Analysing an open cohort stepped-wedge clustered trial with repeated individual binary outcomes

The model

The process I use to simulate the data and then estimate to effects is based on a relatively straightforward logistic regression model with two random effects. To simplify things a bit, I intentionally make the assumption that there are no general time trends that affect that outcomes (though it would not be difficult to add in). In the logistic model, the log-odds (or logit) of a binary outcome is a linear function of predictors and random effects:

\[ \text{logit}(P(y_{ict}=1) = \beta_0 + \beta_1 I_{ct} + b_{ct} + b_i,\] where \(\text{logit}(P(y_{ict}=1))\) is the log-odds for individual \(i\) in cluster (or site) \(c\) during time period \(t\), and \(I_{ct}\) is a treatment indicator for cluster \(c\) during period \(t\).

There are two random effects in this model. The first is a cluster-specific period random effect, \(b_{ct}\) . For each cluster, there will actually be a vector of cluster effects \(\mathbf{b_c} = (b_{c0}, b_{c1},...,b_{c,T-1})\), where \(\mathbf{b_c}\sim MVN(\mathbf{0}, \sigma_{b_c}^2\mathbf{R})\), and \(\mathbf{R}\) is

\[ \mathbf{R} = \left( \begin{matrix} 1 & \rho & \rho^2 & \cdots & \rho^{T-1} \\ \rho & 1 & \rho & \cdots & \rho^{T-2} \\ \rho^2 & \rho & 1 & \cdots & \rho^{T-3} \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ \rho^{T-1} & \rho^{T-2} & \rho^{T-3} & \cdots & 1 \end{matrix} \right ) \]

The second random effect is the individual or patient-level random intercept \(b_i\), where \(b_i \sim N(0,\sigma_{b_i}^2)\). We could assume a more structured relationship for individual patients over time (such as a decaying correlation), but in this application, patients will not have sufficient measurements to properly estimate this.

In the model \(\beta_0\) has the interpretation of the log-odds for the outcome when the the cluster is still in the control state and the cluster-period and individual effects are both 0. \(\beta_1\) is the average treatment effect conditional on the random effects, and is reported as a log odds ratio.

Simulating the study data

I am going to generate a single data set based on this model. If you want more explanation of the code, this earlier post provides the details. The only real difference here is that I am generating an outcome that is a function of cluster-period effects, individual effects, and treatment status.

library(simstudy)

dsite <- genData(24, id = "site")

dper <- addPeriods(dsite, nPeriods = 12, idvars = "site", 
                   perName = "period")
  
dsw <- trtStepWedge(dper, "site", nWaves = 6, lenWaves = 1, 
                    startPer = 4, perName = "period",
                    grpName = "Ict")

siteDef <- defData(varname = "eff.mu", formula = 0, 
                   dist = "nonrandom", id = "site")
siteDef <- defData(siteDef, varname = "eff.s2", formula = 0.3^2, 
                   dist = "nonrandom")

dsw <- addColumns(siteDef, dsw)

dsw <- addCorGen(dsw, nvars = 12, idvar = "site", rho = 0.5, 
                 corstr = "ar1", dist = "normal", 
                 param1 = "eff.mu", param2 = "eff.s2", 
                 cnames = "eff.st")

dsw <- dsw[, .(site, period, startTrt, Ict, eff.st)]

dpat <- genCluster(dper, cLevelVar = "timeID", 
                   numIndsVar = 20, level1ID = "id")

patDef <- defDataAdd(varname = "S0", formula = "0.4;0.4;0.2",
                     dist = "categorical")
patDef <- defDataAdd(patDef, varname = "eff.p", 
                     formula = 0, variance = 0.3^2)

dpat <- addColumns(patDef, dpat)

P <-t(matrix(c( 0.7, 0.2, 0.1, 0.0,
                0.1, 0.3, 0.5, 0.1,
                0.0, 0.1, 0.6, 0.3,
                0.0, 0.0, 0.0, 1.0),
             nrow = 4))

dpat <- addMarkov(dpat, transMat = P, 
                  chainLen = 12, id = "id", 
                  pername = "seq", start0lab = "S0",
                  trimvalue = 4)

dpat[, period := period + seq - 1]
dpat <- dpat[period < 12]

dx <- merge(dpat, dsw, by = c("site","period"))
setkey(dx, id, period)

outDef <- defDataAdd(varname = "y", 
                     formula = "-0.5 - 0.8*Ict + eff.st + eff.p",
                     dist = "binary", link = "logit")

dx <- addColumns(outDef, dx)
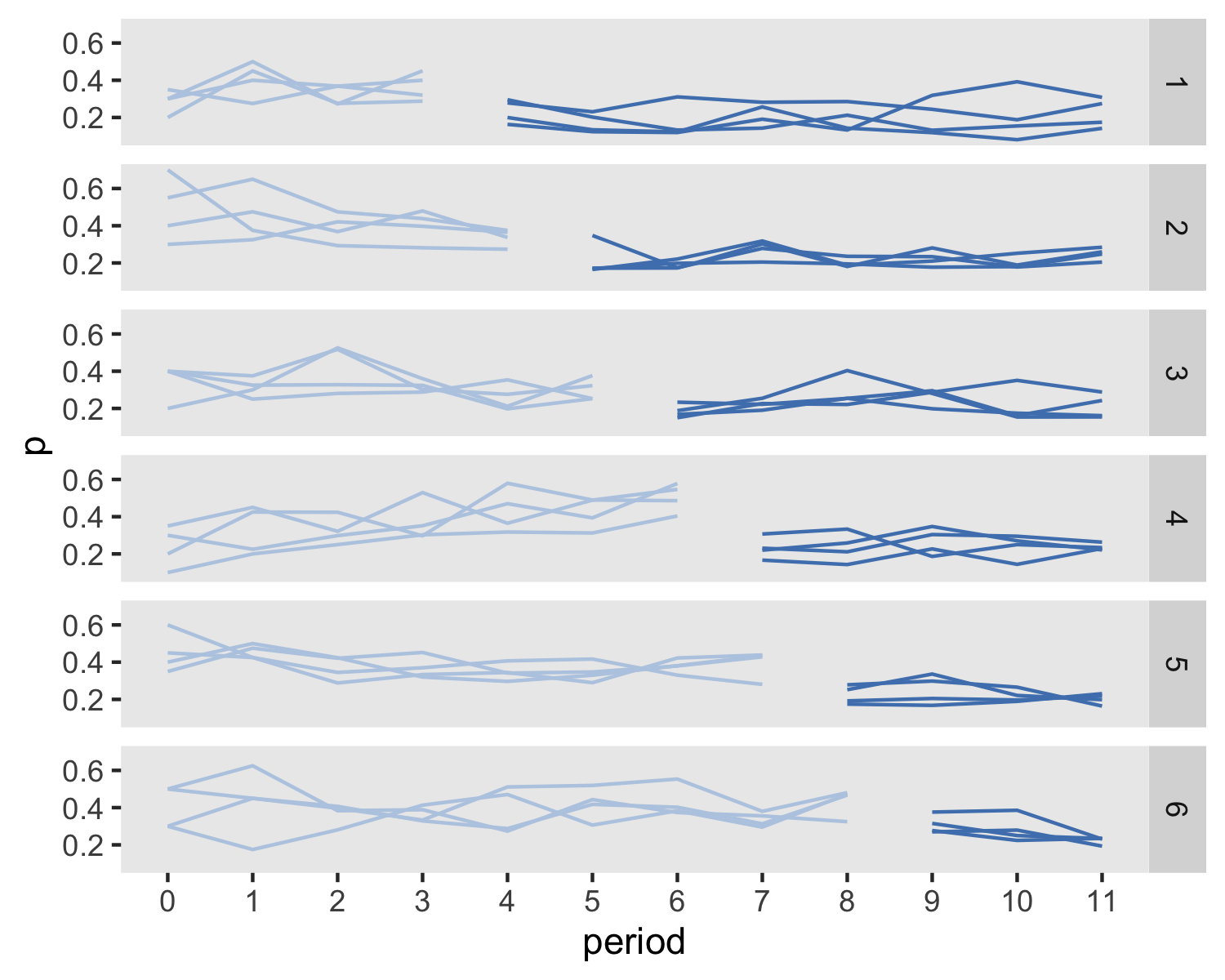
dx <- dx[, .(site, period, id, Ict, y)]

Estimating the treatment effect and variance components

Because none of the maximum likelihood methods implemented in R or SAS could estimate this specific variance structure using a mixed effects logistic regression model, I am fitting a Bayesian model using RStan and Stan, which requires a set of model definitions.

This model specification is actually quite similar to the model I estimated earlier, except of course the outcome distribution is logistic rather than continuous. Another major change is the use of a “non-centered” parameterization, which actually reduced estimation times from hours to minutes (more precisely, about 12 hours to about 30 minutes). This reparameterization requires a Cholesky decomposition of the variance-covariance matrix \(\Sigma\). One additional limitation is that proper convergence of the MCMC chains seems to require a limited prior on \(\rho\), so that \(\rho \sim U(0,1)\) rather than \(\rho \sim U(-1,1)\).

This particular code needs to be saved externally, and I have created a file named binary sw - ar ind effect - non-central.stan. This file is subsequently referenced in the call to RStan.

data {
  int<lower=1> I;              // number of unique individuals
  int<lower=1> N;              // number of records
  int<lower=1> K;              // number of predictors
  int<lower=1> J;              // number of sites
  int<lower=0> T;              // number of periods
  int<lower=1,upper=I> ii[N];  // id for individual
  int<lower=1,upper=J> jj[N];  // group for individual
  int<lower=1,upper=T> tt[N];  // period of indidvidual
  matrix[N, K] x;              // matrix of predictors
  int<lower=0,upper=1> y[N];   // vector of binary outcomes
}

parameters {
  vector[K] beta;              // model fixed effects
  real<lower=0> sigma_S;       // site variance (sd)
  real<lower=0,upper=1> rho;   // correlation
  real<lower=0> sigma_I;       // individual level varianc (sd)
  
  // non-centered paramerization
  
  vector[T] z_ran_S[J];   // site level random effects (by period)
  vector[I] z_ran_I;      // individual level random effects        
}

transformed parameters {

  cov_matrix[T] Sigma;
  matrix[T, T] L;         // for non-central parameterization
  vector[I] ran_I;        // individual level random effects
  vector[T] ran_S[J];     // site level random effects (by period)
  vector[N] yloghat;

  // Random effects with exchangeable correlation

  real sigma_S2 = sigma_S^2;

  for (j in 1:T)
    for (k in 1:T)
      Sigma[j,k] = sigma_S2 * pow(rho,abs(j-k));
  
  // for non-centered parameterization
  
  L = cholesky_decompose(Sigma);

  for(j in 1:J)
    ran_S[j] = L * z_ran_S[j];
    
  ran_I = sigma_I * z_ran_I;
  
  // defining mean on log-odds scale

  for (i in 1:N)
      yloghat[i] = x[i]*beta + ran_S[jj[i], tt[i]] + ran_I[ii[i]];
      
}

model {
  
  sigma_I ~ exponential(0.25);
  sigma_S ~ exponential(0.25);
  
  rho ~ uniform(0, 1);
  
  for(j in 1:J) {
    z_ran_S[j] ~ std_normal();
  }

  z_ran_I ~ std_normal();
  
  y ~ bernoulli_logit(yloghat);

}

Set up the data and call stan from R

Just for completeness, I am providing the code that shows the interface between R and Stan using RStan. The data needs to be sent to Stan as a list of data elements, which here is called testdat. For the estimation of the posterior probabilities, I am specifying 4 chains of 4000 iterations each, which includes 1000 warm-up iterations. I specified “adapt_delta = 0.90” to reduce the step-size a bit (default is 0.80); this slows things down a bit, but improves stability.

As I mentioned earlier, with this data set (and rather large number of effects to estimate), the running time is between 30 and 45 minutes. One of the downsides of this particular Bayesian approach is that it wouldn’t really be practical to do any kind of sample size estimate.

x <- as.matrix(dx[ ,.(1, Ict)])
I <- dx[, length(unique(id))]
N <- nrow(x)
K <- ncol(x)
J <- dx[, length(unique(site))]
T <- dx[, length(unique(period))]
ii <- dx[, id]
jj <- dx[, site]
tt <- dx[, period] + 1
y <- dx[, y]

testdat <- list(I=I, N=N, K=K, J=J, T=T, ii=ii, jj=jj, tt=tt, x=x, y=y)

library(rstan)
options(mc.cores = parallel::detectCores())

rt <- stanc("binary sw - ar ind effect - non-central.stan")
sm <- stan_model(stanc_ret = rt, verbose=FALSE)

fit.ar1 <- sampling(sm, data=testdat,
                    iter = 4000, warmup = 1000,
                    control=list(adapt_delta=0.90,
                        max_treedepth = 15),
                    chains = 4)

Diagnostics

After running the MCMC process to generate the probability distributions, the trace plots show that the mixing is quite adequate for the chains.

plot(fit.ar1, plotfun = "trace", pars = pars, 
  inc_warmup = FALSE, ncol = 1)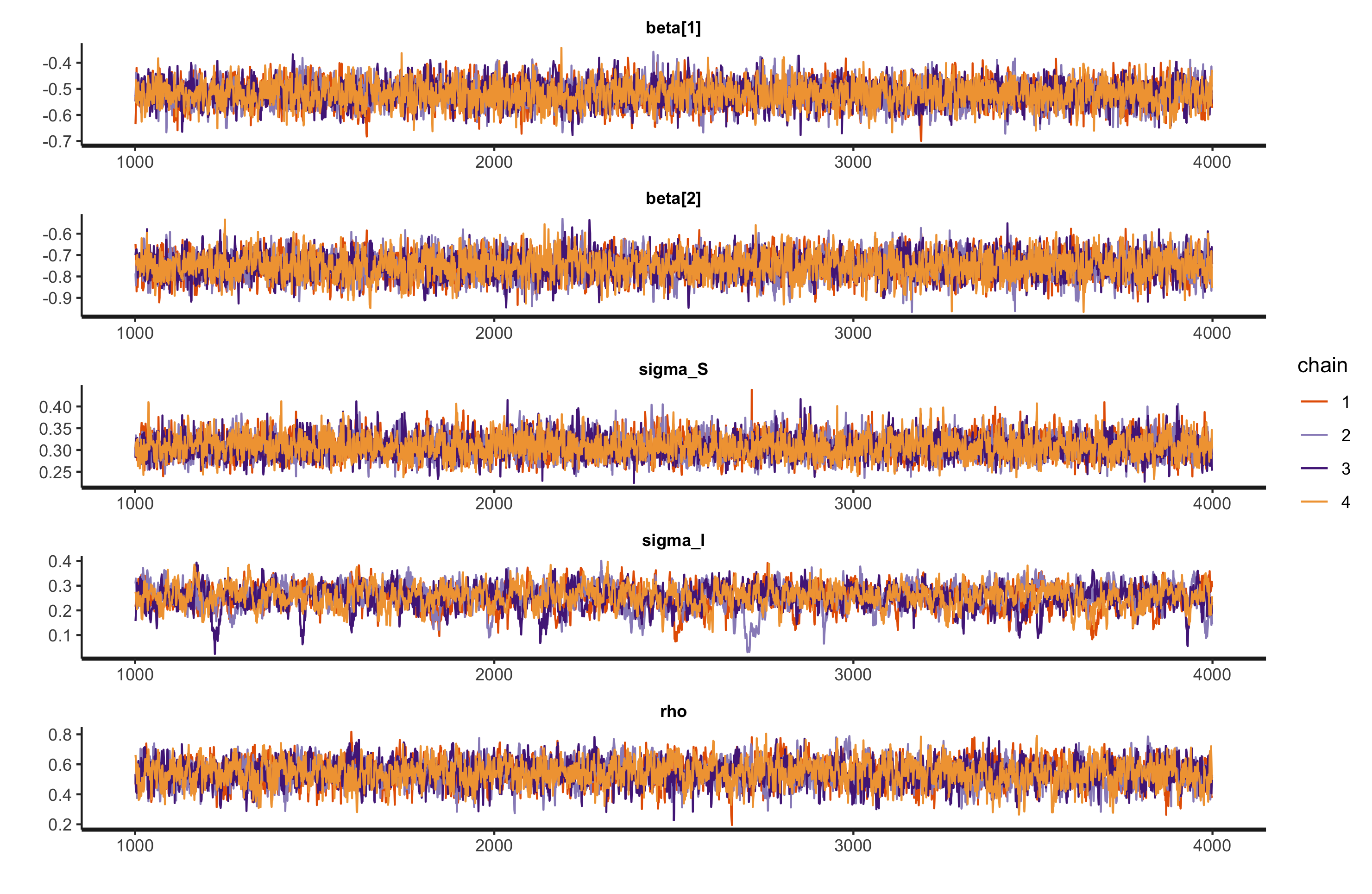

Extracting results

If we take a look at the posterior probability distributions, we can see that they contain the original values used to generate the data - so at least in this case, the model seems to model the original data generation process quite well.

pars <- c("beta", "sigma_S","sigma_I","rho")
summary(fit.ar1, pars = pars, probs = c(0.025, 0.975))$summary

##           mean  se_mean     sd   2.5%  97.5% n_eff Rhat
## beta[1] -0.519 0.000687 0.0459 -0.609 -0.428  4470    1
## beta[2] -0.751 0.000844 0.0573 -0.864 -0.638  4618    1
## sigma_S  0.307 0.000394 0.0256  0.260  0.362  4223    1
## sigma_I  0.254 0.001548 0.0476  0.148  0.337   945    1
## rho      0.544 0.001594 0.0812  0.376  0.698  2599    1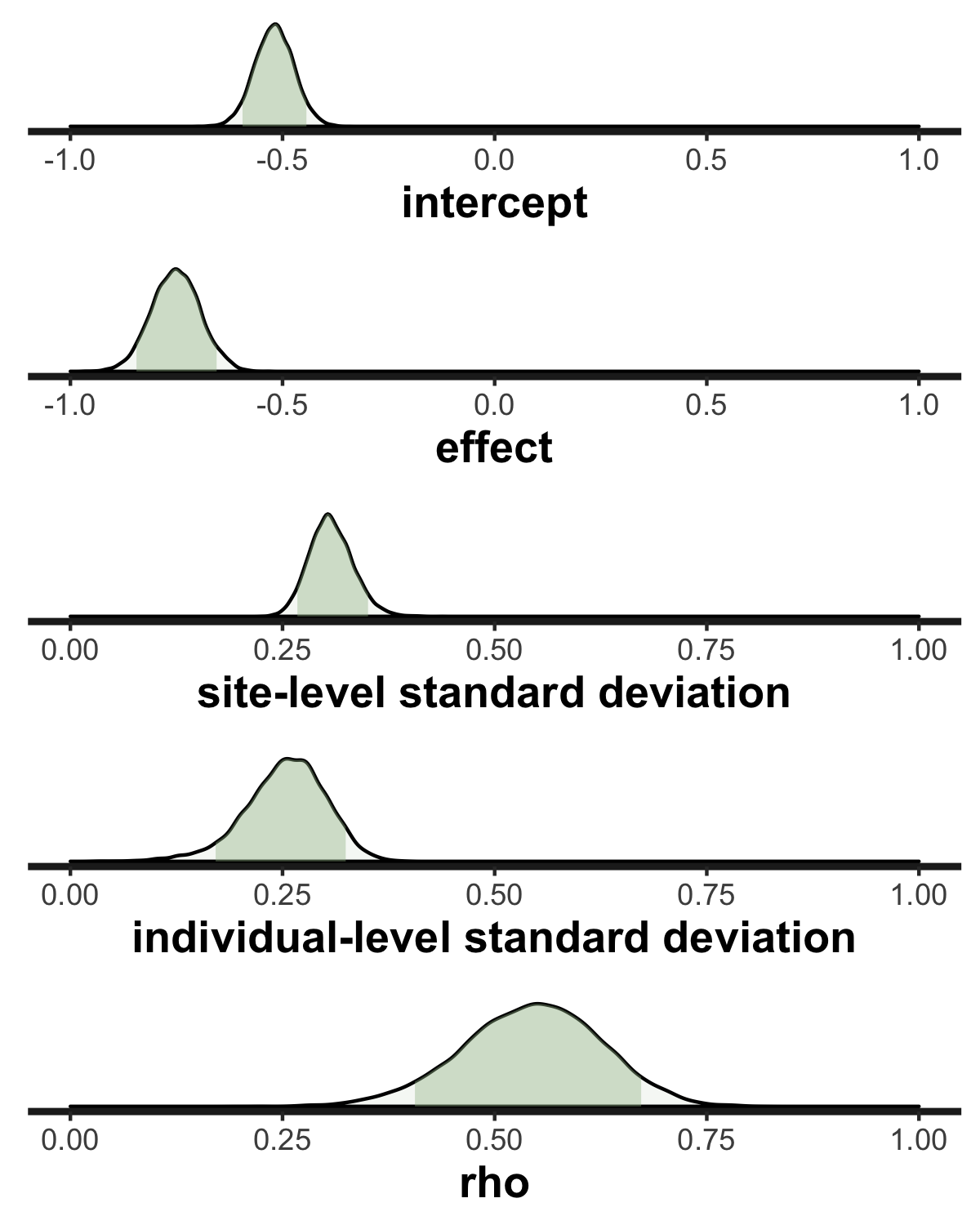

One thing that is not working so well is my attempt to compare different models. For example, I might want to fit another model that does not assume between-period correlations decay and compare it to the current model. Previously, I used the bridgesampling package for the comparisons, but it does not seem to be able to accommodate these models. I will continue to explore the options more model comparison and will report back if I find something promising.