The federal government recently granted emergency approval for the use of antibody rich blood plasma when treating hospitalized COVID-19 patients. This announcement is unfortunate, because we really don’t know if this promising treatment works. The best way to determine this, of course, is to conduct an experiment, though this approval makes this more challenging to do; with the general availability of convalescent plasma (CP), there may be resistance from patients and providers against participating in a randomized trial. The emergency approval sends the incorrect message that the treatment is definitively effective. Why would a patient take the risk of receiving a placebo when they have almost guaranteed access to the therapy?
This doesn’t obviate the fact that we still need to figure out if CP is effective. Last month, I described an approach to pooling data across multiple different, but similar, studies as way to leverage information that is being generated around the country and world from ongoing trials. I was particularly cryptic about the nature of the research, because the paper describing the details of the proposed research had not yet been published. Now, the project has a name (COMPILE), a website, and most importantly, participating studies committed to sharing data.
In preparation for the analyses, we have been developing a statistical plan, which is based on a pooled Bayesian model similar to what I described) earlier. The Bayesian approach offers much needed flexibility in this context when we must make a principled decision as quickly as possible. Indeed, now that the emergency approval has been granted, there is even more urgency. The study’s Data Safety and Monitoring Board will be evaluating the data frequently, which a Bayesian approach accommodates quite well. (I imagine I will have much to write about over the next few months as we try to better understand the implications and challenges of taking this path.)
In this post, I am describing a nitty-gritty issue related to Markov chain Monte Carlo (MCMC) estimation: stability. It may not sound super-exciting, but stable estimation is key to drawing correct inferences from the estimated posterior distribution. As a model becomes more complex, the MCMC estimation in stan can be plagued by degenerate sampling caused by divergent transitions. MCMC works well when the algorithm takes the sampler across the full posterior distribution without getting stuck, but all bets are off when the process breaks down.
Using a slightly simplified version of the data and model we are proposing for COMPILE, I want to show how to see if things have gotten stuck at some point, and then present a possible solution to getting things unstuck. (I highly encourage you to look here and here for many more details if this is indeed exciting to you.)
The model
The studies included in this meta-analysis will be similar in that they are all providing 1- or 2-units of plasma to the patients randomized to therapy. However, there will be differences with respect to the control arm: studies will use a saline solution, non-convalescent plasma, or usual care (in the last case, the study is not blinded). We need to account for the possibility that the treatment effect will vary slightly depending on the type of control. In this case, I am assuming a binary outcome (though in the actual study we are using an ordinal outcome and a proportional odds model). Here is the logistic model: \[\text{logodds}(P(y_{ik}=1)) = \alpha_0 + b_k + \delta_k x_{ik}\] where the observed data are \(y_{ik}\), the indicator for the outcome (say death) of patient \(i\) in study \(k\), and \(x_{ik}\), an indicator set to \(1\) if the patient is in the control arm, 0 otherwise. The parameters are \(\alpha_0\), the global logodds of death (note here the intercept represents the treatment condition, not the control condition as is usually the case); \(b_k\), the study-specific logodds of death given treatment; and \(\delta_k\), the “control” effect (a logodds ratio) specific to study \(k\).
The really interesting aspect of this model is \(\delta_k\). This effect is a function of three components - the study site, the control-type, and the the overall/global treatment effect. We are assuming that there is a tendency for studies to vary around a control-type effect average. So, with three controls \(c\in {1,2,3}\): \[\delta_k \sim N(\delta_c, \eta_0),\]
determined by the control-type of study \(k\). Furthermore, we assume that the control-type effects, the \(\delta_c\)’s, vary around a global effect \(\Delta\): \[\delta_c \sim N(\Delta, \eta).\] We assume that \(\eta\) is quite small; that is, the control effects will likely be very similar. We are not actually interested in \(\eta\) so we do not attempt to estimate it. However \(\eta_0\), the variability across studies, is important, so we will estimate that.
Generating data
To start, here are the R packages I am using to generate the data.
library(simstudy)
library(data.table)Next, I define the study level parameters: the study-specific intercept \(b_k\) and the study-specific “control” effect \(\delta_k\), which is a function of the control-type. Note I do not specify a study-level “control” effect, there will just be natural variation across studies. The individual-level outcome \(y_{ik}\) is defined as a function of study parameters. The overall treatment effect is \(\Delta = 0.5\) on the logodds ratio scale.
def_s <- defDataAdd(varname = "b_k", formula = 0, variance = 0.025)
def_s <- defDataAdd(
def_s, varname = "delta_k",
formula = "(c_type==1) * 0.4 + (c_type==2) * 0.5 + (c_type==3) * 0.6",
dist = "nonrandom"
)
def_i <- defDataAdd(
varname = "y", formula = "-1 + b_k + rx * delta_k",
dist = "binary", link = "logit")I am generating 7 studies with under each control type, for a total of 21 studies. Each study has 50 patients, 25 in each arm, for a total of 1050 patients.
dc <- genData(3, id = "c_type")
ds <- genCluster(dc, "c_type", numIndsVar = 7, level1ID = "site")
ds <- addColumns(def_s, ds)
di <- genCluster(ds, "site", 50, "id")
di <- trtAssign(di, 2, strata = "site", grp = "rx")
di <- addColumns(def_i, di)Estimation using stan
I am using rstan directly to sample from the posterior distribution, as opposed to using a more user-friendly package like brms or rstanarm. I’ve actually been warned against taking this approach by folks at stan, because it can be more time consuming and could lead to problems of the sort that I am showing you how to fix. However, I find building the model using stan code very satisfying and illuminating; this process has really given me a much better appreciation of the Bayesian modeling. And besides, this model is odd enough that trying to shoehorn it into a standard brms model might be more trouble than it is worth.
library(rstan)
library(ggplot)
library(bayesplot)The stan code, which can reside in its own file, contains a number of blocks that define the model. The data block specifies the data will be provided to the model; this can include summary data as well as raw data. The parameters block is where you specify the parameters of the model that need to be estimated. The transformed parameters block includes another set of parameters that will be estimated, but are a function of parameters defined in the previous block. And in this case, the last block is the model where prior distributions are specified as well as the likelihood (outcome) model. Rather than walk you through the details here, I will let you study a bit and see how this relates to the model I specified above.
data {
int<lower=0> N; // number of observations
int<lower=0> C; // number of control types
int<lower=1> K; // number of studies
int y[N]; // vector of categorical outcomes
int<lower=1,upper=K> kk[N]; // site for individual
int<lower=0,upper=1> ctrl[N]; // treatment or control
int<lower=1,upper=C> cc[K]; // specific control for site
}
parameters {
real alpha; // overall intercept for treatment
vector[K] beta_k; // site specific intercept
real<lower=0> sigma_b; // sd of site intercepts
vector[K] delta_k; // site specific treatment effect
real<lower=0> eta_0; // sd of delta_k (around delta_c)
vector[C] delta_c; // control-specific effect
real Delta; // overall control effect
}
transformed parameters{
vector[N] yhat;
for (i in 1:N)
yhat[i] = alpha + beta_k[kk[i]] + (ctrl[i] * (delta_k[kk[i]]));
}
model {
// priors
alpha ~ student_t(3, 0, 2.5);
beta_k ~ normal(0, sigma_b);
sigma_b ~ cauchy(0, 1);
eta_0 ~ cauchy(0, 1);
for (k in 1:K)
delta_k[k] ~ normal(delta_c[cc[k]], eta_0);
delta_c ~ normal(Delta, 0.5);
Delta ~ normal(0, 10);
// likelihood/outcome model
y ~ bernoulli_logit(yhat);
}We need to compile the stan code so that it can be called from the R script:
rt_c <- stanc("binary_outcome.stan")
sm_c <- stan_model(stanc_ret = rt_c, verbose=FALSE)And here is the R code that prepares the data for the stan program and then samples from the posterior distribution. In this case, I will be using 4 different Monte Carlo chains of 2500 draws each (after allowing for 500 warm-up draws), so we will have a actual sample size of 10,000.
N <- nrow(di) ;
C <- di[, length(unique(c_type))]
K <- di[, length(unique(site))]
y <- as.numeric(di$y)
kk <- di$site
ctrl <- di$rx
cc <- di[, .N, keyby = .(site, c_type)]$c_type
sampdat <- list(N=N, C=C, K=K, y=y, kk=kk, ctrl=ctrl, cc=cc)
fit_c <- sampling(
sm_c, data = sampdat, iter = 3000, warmup = 500,
show_messages = FALSE, cores = 4, refresh = 0,
control = list(adapt_delta = 0.8)
)Inspecting the posterior distribution
Assuming that everything has run smoothly, the first thing to do is to make sure that the MCMC algorithm adequately explored the full posterior distribution in the sampling process. We are typically interested in understanding the properties of the distribution, like the mean or median, or 95% credible intervals. To have confidence that these properties reflect the true posterior probabilities, we need to be sure that the sample they are drawn from is a truly representative one.
A quick and effective way to assess the “representativeness” of the sample is to take a look at the trace plot for a particular parameter, which literally tracks the path of the MCMC algorithm through the posterior distribution. Below, I’ve included two trace plots, one for \(\Delta\), the overall effect, and the other for \(\eta_0\), the variability of a study’s control effect \(\delta_k\) around \(\delta_c\). On the left, the plots appear as they should, with lines jumping up and down. However, these particular plots include red indicators where the algorithm got stuck, where there were divergent transitions. We really don’t want to see any of this indicators, because that is a sign that our sample is not representative of the posterior distribution.
posterior_c <- as.array(fit_c)
lp_c <- log_posterior(fit_c)
np_c <- nuts_params(fit_c)
color_scheme_set("mix-brightblue-gray")
mcmc_trace(posterior_c, pars = "Delta", np = np_c) +
xlab("Post-warmup iteration")
mcmc_trace(
posterior_c, pars = "Delta", np = np_c, window = c(1500, 1700)
) +
xlab("Post-warmup iteration")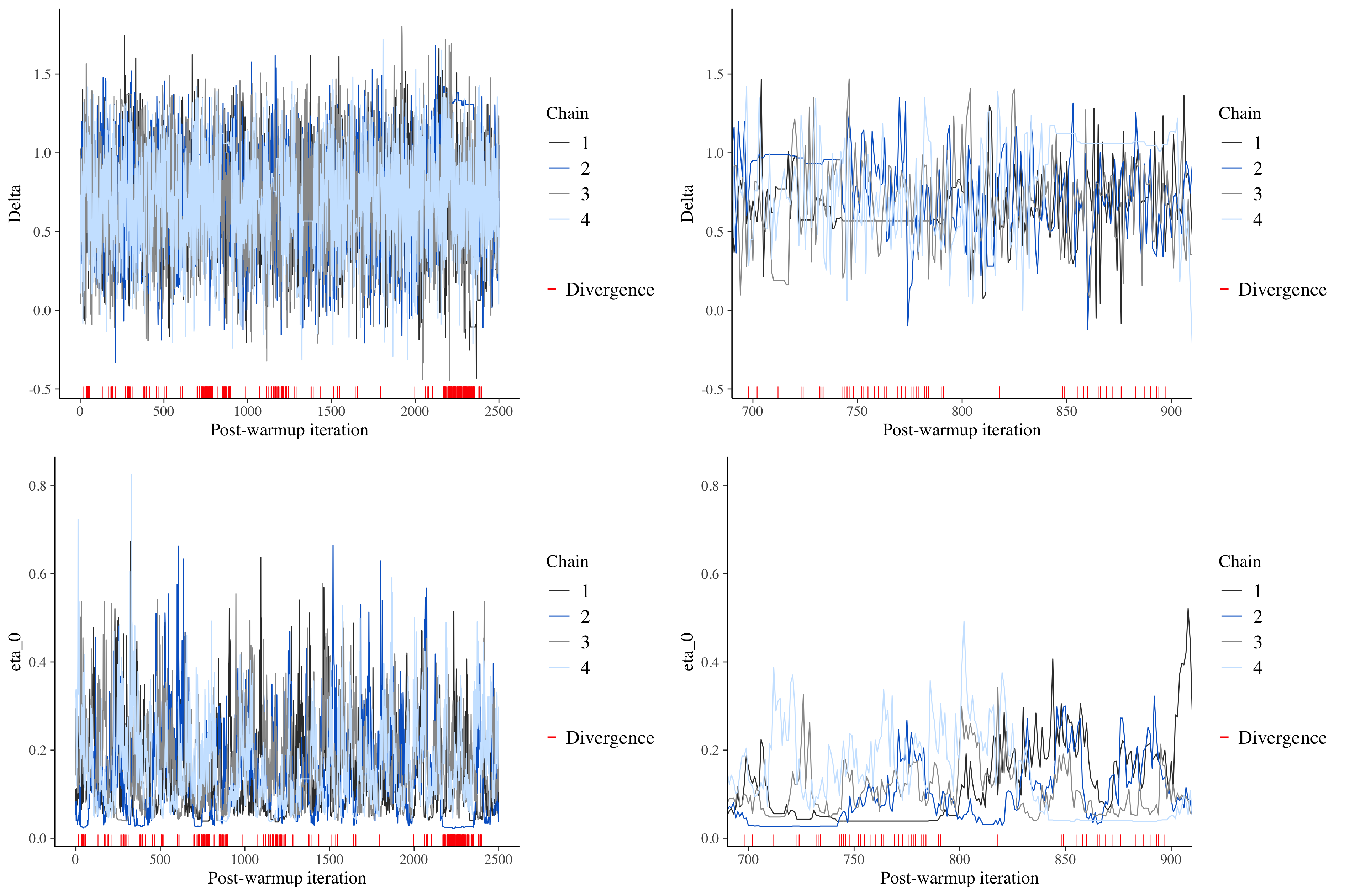
On the right in the figure above, I’ve zoomed in on steps 700 to 900 to see if we can see any patterns. And sure enough, we can. In the \(\Delta\) plot, straight lines appear in the middle, evidence that the sampling for some of the chains did indeed get stuck. Likewise, the plot for \(\eta_0\) shows flat lines near \(0\).
There’s an additional plot that shows the same thing but in a slightly more dramatic and comprehensive way. This plot (shown below) has a line for each step connecting the parameter estimates of that step. The red lines represent divergent transitions. The important thing to note here is that in all cases with divergent transitions, \(\eta_0\) found itself close to \(0\). In other words, the sampling was getting stuck at this point, and this is the likely culprit for the sampling issues.
color_scheme_set("darkgray")
parcoord_c <-mcmc_parcoord(
posterior_c, np = np_c,
pars = c("eta_0", "sigma_b", "alpha",
"delta_c[1]", "delta_c[2]","delta_c[3]", "Delta")
)
parcoord_c +
scale_x_discrete(expand = c(0.01, 0.01)) +
theme(panel.background = element_rect(fill = "grey90")) +
ylim(-3, 3) +
ggtitle("Original model specification")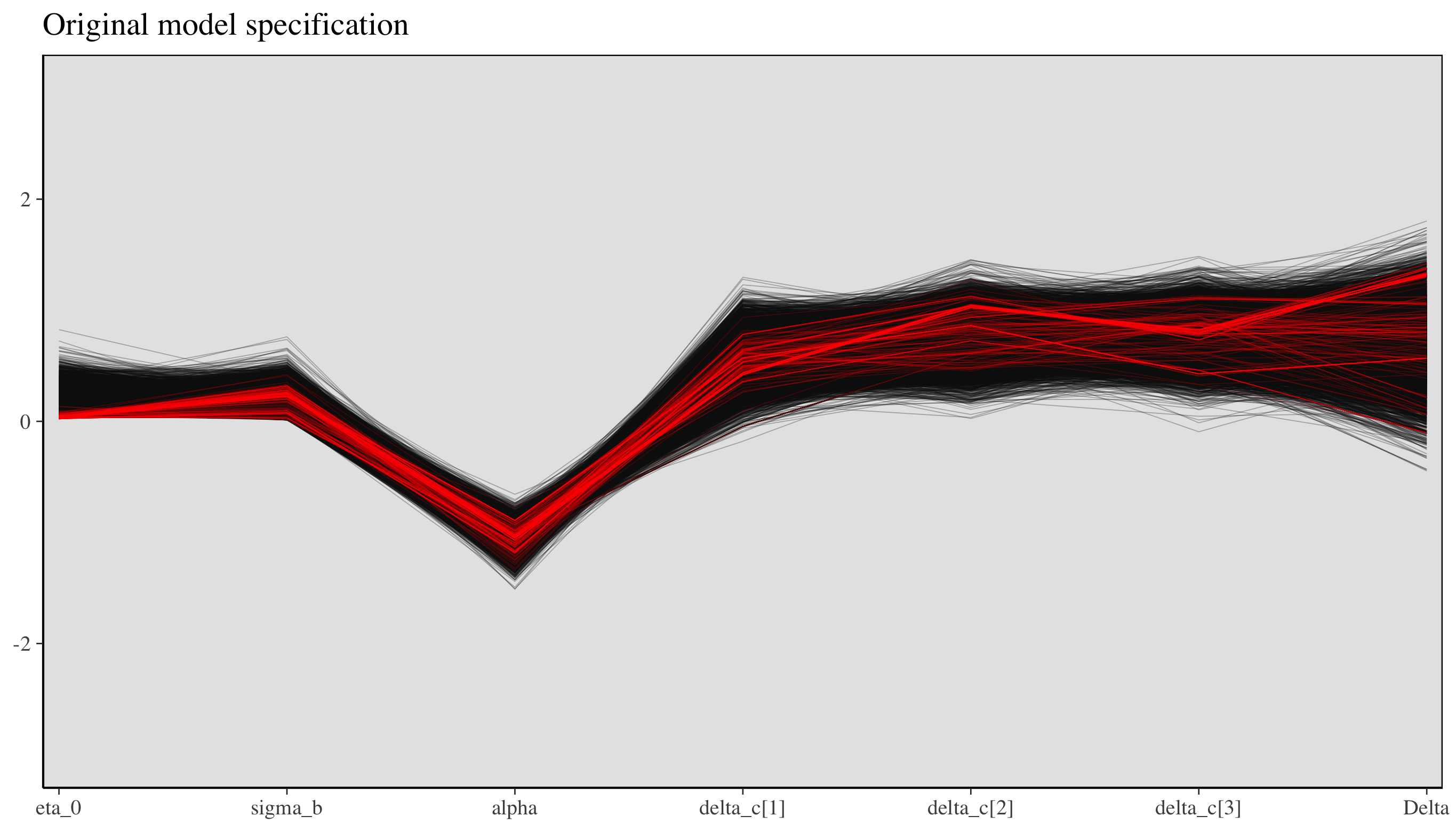
A remedy for divergent transitions
In a moment, I will provide a brief illustration of the perils of divergent transitions, but before that I want to describe “non-centered parameterization,” an approach that can be used to mitigate divergence. The idea is that since sampling from a standard Gaussian or normal distribution is less likely to lead to problematic transitions, we should try to do this as much as possible. “In a non-centered parameterization we do not try to fit the group-level parameters directly, rather we fit a latent Gaussian variable from which we can recover the group-level parameters with a scaling and a translation.” (See here for the source of this quote and much more.)
For example, in the original model specification, we parameterized \(\delta_k\) and \(\delta_c\) as
\[ \delta_k \sim N(\delta_c, \eta_0) \\ \delta_c \sim N(\Delta, 0.5) \]
\[ \eta_0 \sim Cauchy(0, 1) \\ \Delta \sim N(0, 10), \]
whereas using “non-centered” parameterization, we would incorporate two latent standard normal variables \(\theta_{rx}\) and \(\theta_c\) into the model. \(\delta_k\) and \(\delta_c\) have the same prior distribution as the original model, but we are now sampling from standard normal prior distribution: \[ \delta_k = \delta_c + \eta_0 \theta_{rx} \\ \theta_{rx} \sim N(0, 1) \]
\[ \delta_c = \Delta + 0.5\theta_c\\ \theta_c \sim N(0, 1) \]
\[ \eta_0 \sim Cauchy(0, 1) \\ \Delta \sim N(0, 10). \]
This transformation makes the path through the posterior distribution much smoother and, at least in this case, eliminates the divergent transitions.
Here is the stan code using non-centered parameterization (again, feel free to linger and study):
data {
int<lower=0> N; // number of observations
int<lower=0> C; // number of control types
int<lower=1> K; // number of studies
int y[N]; // vector of categorical outcomes
int<lower=1,upper=K> kk[N]; // site for individual
int<lower=0,upper=1> ctrl[N]; // treatment or control
int<lower=1,upper=C> cc[K]; // specific control for site
}
parameters {
real alpha; // overall intercept for treatment
real<lower=0> sigma_b;
real<lower=0> eta_0; // sd of delta_k (around delta)
real Delta; // overall control effect
// non-centered parameterization
vector[K] z_ran_rx; // site level random effects (by period)
vector[K] z_ran_int; // individual level random effects
vector[C] z_ran_c; // individual level random effects
}
transformed parameters{
vector[N] yhat;
vector[K] beta_k;
vector[K] delta_k; // site specific treatment effect
vector[C] delta_c;
beta_k = sigma_b * z_ran_int + alpha;
for (i in 1:C)
delta_c[i] = 0.5 * z_ran_c[i] + Delta;
for (i in 1:K)
delta_k[i] = eta_0 * z_ran_rx[i] + delta_c[cc[i]];
for (i in 1:N)
yhat[i] = beta_k[kk[i]] + ctrl[i] * delta_k[kk[i]];
}
model {
// priors
alpha ~ student_t(3, 0, 2.5);
z_ran_c ~ std_normal();
z_ran_int ~ std_normal();
z_ran_rx ~ std_normal();
sigma_b ~ cauchy(0, 1);
eta_0 ~ cauchy(0, 1);
Delta ~ normal(0, 10);
// outcome model
y ~ bernoulli_logit(yhat);
}Looking at the trace plots from the non-centered model makes it clear that divergent transitions are no longer a problem. There are no red indicators, and the patterns of straight lines have been eliminated:
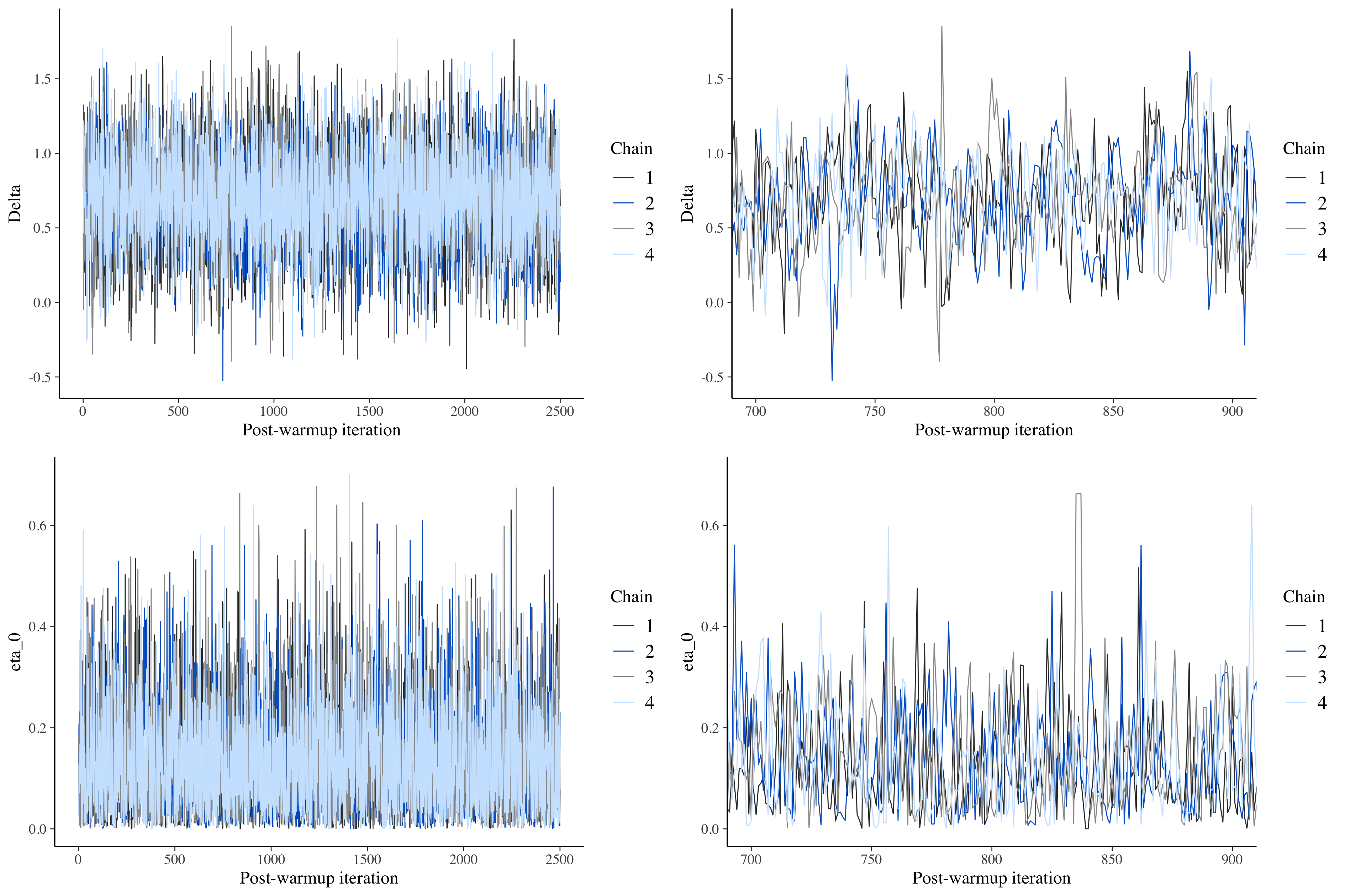
Proceed with caution if you ignore the divergence warnings
If we don’t heed the warnings, how bad can things be? Well, it will probably depend on the situation, but after exploring with multiple data sets, I have convinced myself that it is probably a good idea to reduce the number of divergent transitions as close to 0 as possible.
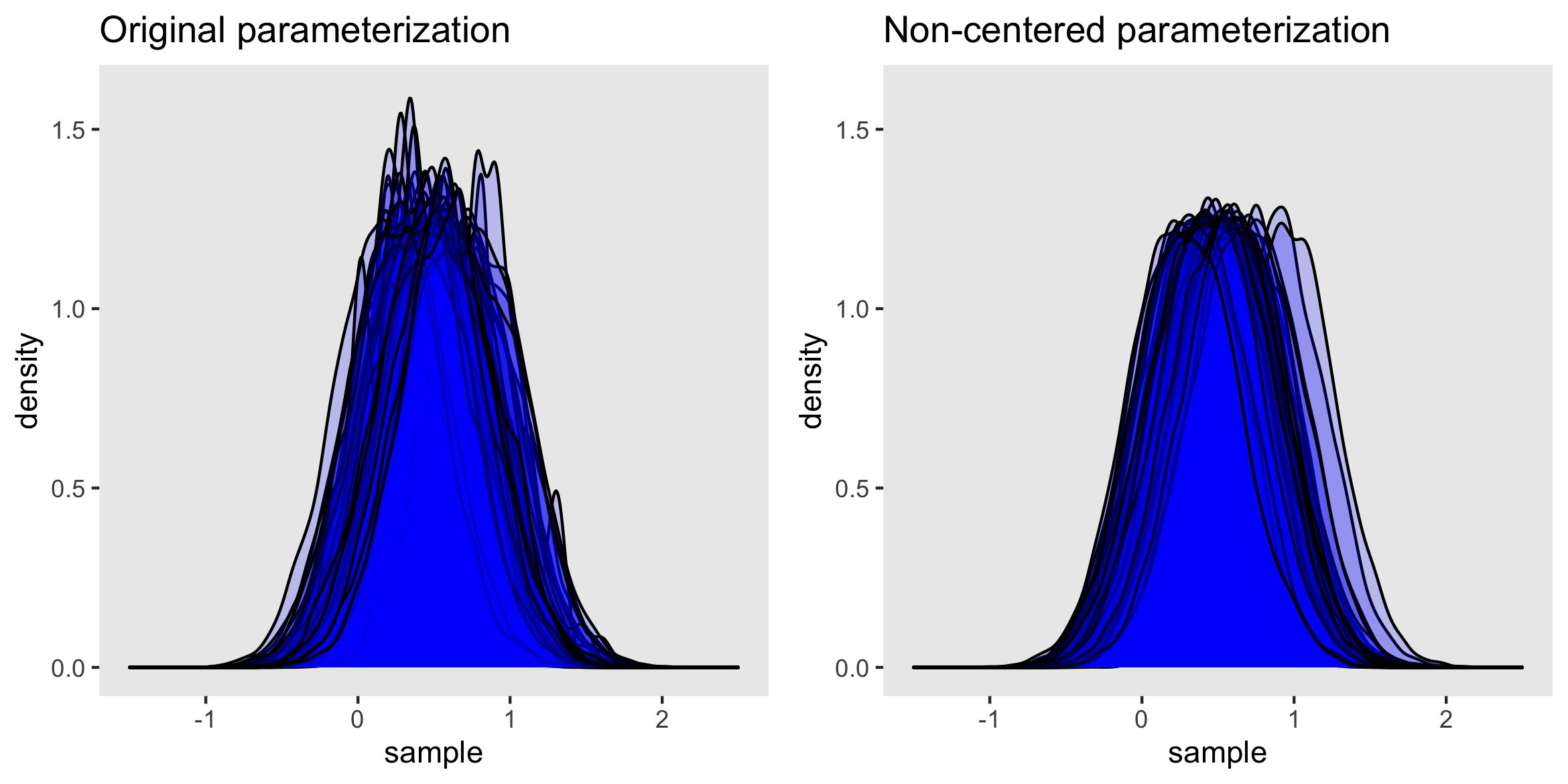
I conducted an experiment by generating 100 data sets and fitting a model using both the original and non-centered parameterizations. I collected the posterior distribution for each data set and estimation method, and plotted the density curves. (In case you are interested, I used a parallel process running on a high-performance computing core to do this; running on my laptop, this would have taken about 5 hours, but on the HPC it ran in under 15 minutes.) The purpose of this was to explore the shapes of the densities across the different data sets. I know it is a little odd to use this frequentist notion of repeatedly sampling datasets to evaluate the performance of these two approaches, but I find it to be illuminating. (If you’re interested in the code for that, let me know.)
Below on the right, the plot of the posteriors from the non-centered parameterization shows variability in location, but is otherwise remarkably consistent in shape and scale. On the left, posterior densities show much more variation; some are quite peaked and others are even bi-modal. (While I am not showing this here, the densities from samples with more divergent transitions tend to diverge the most from the well-behaved densities on the right.)
Although the mean or median estimates from a divergent sample may not be too far off from its non-divergent counterpart, the more general description of the distribution may be quite far off the mark, making it likely that inferences too will be off the mark.