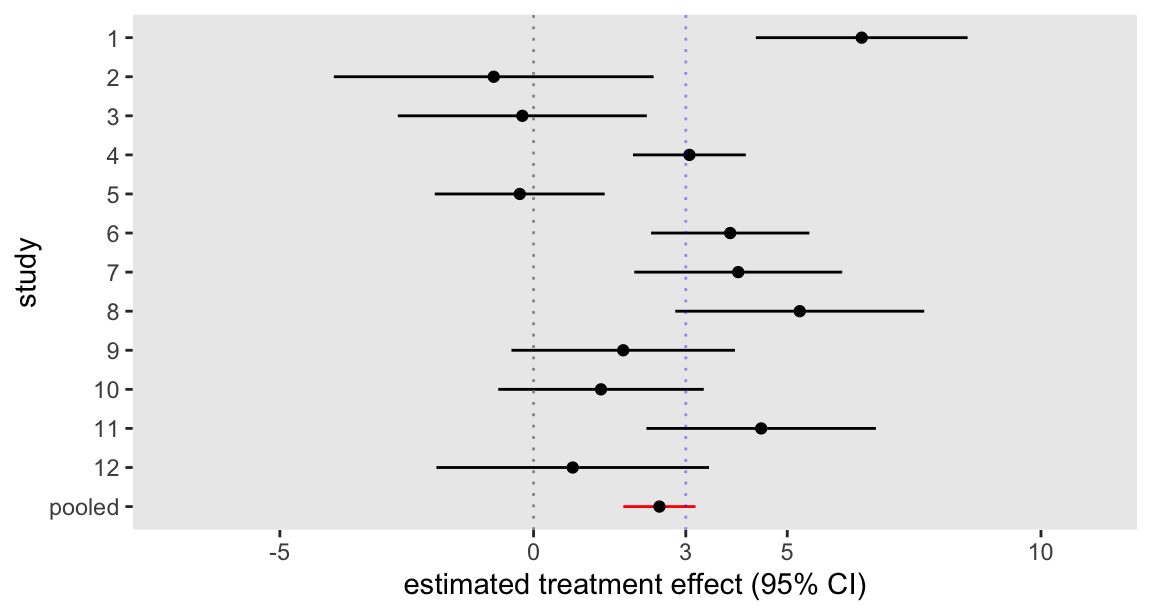
This is essentially an addendum to the previous post where I simulated data from multiple RCTs to explore an analytic method to pool data across different studies. In that post, I used the nlme package to conduct a meta-analysis based on individual level data of 12 studies. Here, I am presenting an alternative hierarchical modeling approach that uses the Bayesian package rstan.
Create the data set
We’ll use the exact same data generating process as described in some detail in the previous post.
library(simstudy)
library(rstan)
library(data.table)defS <- defData(varname = "a.k", formula = 3, variance = 2, id = "study")
defS <- defData(defS, varname = "d.0", formula = 3, dist = "nonrandom")
defS <- defData(defS, varname = "v.k", formula = 0, variance = 6, dist= "normal")
defS <- defData(defS, varname = "s2.k", formula = 16, variance = .2, dist = "gamma")
defS <- defData(defS, varname = "size.study", formula = ".3;.5;.2", dist = "categorical")
defS <- defData(defS, varname = "n.study",
formula = "(size.study==1) * 20 + (size.study==2) * 40 + (size.study==3) * 60",
dist = "poisson")
defI <- defDataAdd(varname = "y", formula = "a.k + x * (d.0 + v.k)", variance = "s2.k")
RNGkind(kind = "L'Ecuyer-CMRG")
set.seed(12764)
ds <- genData(12, defS)
dc <- genCluster(ds, "study", "n.study", "id", )
dc <- trtAssign(dc, strata = "study", grpName = "x")
dc <- addColumns(defI, dc)
d.obs <- dc[, .(study, id, x, y)]Build the Stan model
There are multiple ways to estimate a Stan model in R, but I choose to build the Stan code directly rather than using the brms or rstanarm packages. In the Stan code, we need to define the data structure, specify the parameters, specify any transformed parameters (which are just a function of the parameters), and then build the model - which includes laying out the prior distributions as well as the likelihood.
In this case, the model is slightly different from what was presented in the context of a mixed effects model. This is the mixed effects model:
\[ y_{ik} = \alpha_k + \delta_k x_{ik} + e_{ik} \\ \\ \delta_k = \delta_0 + v_k \\ e_{ik} \sim N(0, \sigma_k^2), v_k \sim N(0,\tau^2) \] In this Bayesian model, things are pretty much the same: \[ y_{ik} \sim N(\alpha_k + \delta_k x_{ik}, \sigma_k^2) \\ \\ \delta_k \sim N(\Delta, \tau^2) \]
The key difference is that there are prior distributions on \(\Delta\) and \(\tau\), introducing an additional level of uncertainty into the estimate. I would expect that the estimate of the overall treatment effect \(\Delta\) will have a wider 95% CI (credible interval in this context) than the 95% CI (confidence interval) for \(\delta_0\) in the mixed effects model. This added measure of uncertainty is a strength of the Bayesian approach.
data {
int<lower=0> N; // number of observations
int<lower=1> K; // number of studies
real y[N]; // vector of continuous outcomes
int<lower=1,upper=K> kk[N]; // study for individual
int<lower=0,upper=1> x[N]; // treatment arm for individual
}
parameters {
vector[K] beta; // study-specific intercept
vector[K] delta; // study effects
real<lower=0> sigma[K]; // sd of outcome dist - study specific
real Delta; // average treatment effect
real <lower=0> tau; // variation of treatment effects
}
transformed parameters{
vector[N] yhat;
for (i in 1:N)
yhat[i] = beta[kk[i]] + x[i] * delta[kk[i]];
}
model {
// priors
sigma ~ normal(0, 2.5);
beta ~ normal(0, 10);
tau ~ normal(0, 2.5);
Delta ~ normal(0, 10);
delta ~ normal(Delta, tau);
// outcome model
for (i in 1:N)
y[i] ~ normal(yhat[i], sigma[kk[i]]);
}Generate the posterior distributions
With the model in place, we transform the data into a list so that Stan can make sense of it:
N <- nrow(d.obs) ## number of observations
K <- dc[, length(unique(study))] ## number of studies
y <- d.obs$y ## vector of continuous outcomes
kk <- d.obs$study ## study for individual
x <- d.obs$x ## treatment arm for individual
ddata <- list(N = N, K = K, y = y, kk = kk, x = x)And then we compile the Stan code:
rt <- stanc("model.stan")
sm <- stan_model(stanc_ret = rt, verbose=FALSE)Finally, we can sample data from the posterior distribution:
fit <- sampling(sm, data=ddata, seed = 3327, iter = 10000, warmup = 2500,
control=list(adapt_delta=0.9))Check the diagonstic plots
Before looking at any of the output, it is imperative to convince ourselves that the MCMC process was a stable one. The trace plot is the most basic way to assess this. Here, I am only showing these plots for \(\Delta\) and \(\tau\), but the plots for the other parameters looked similar, which is to say everything looks good:
pname <- c("Delta", "tau")
stan_trace(object = fit, pars = pname)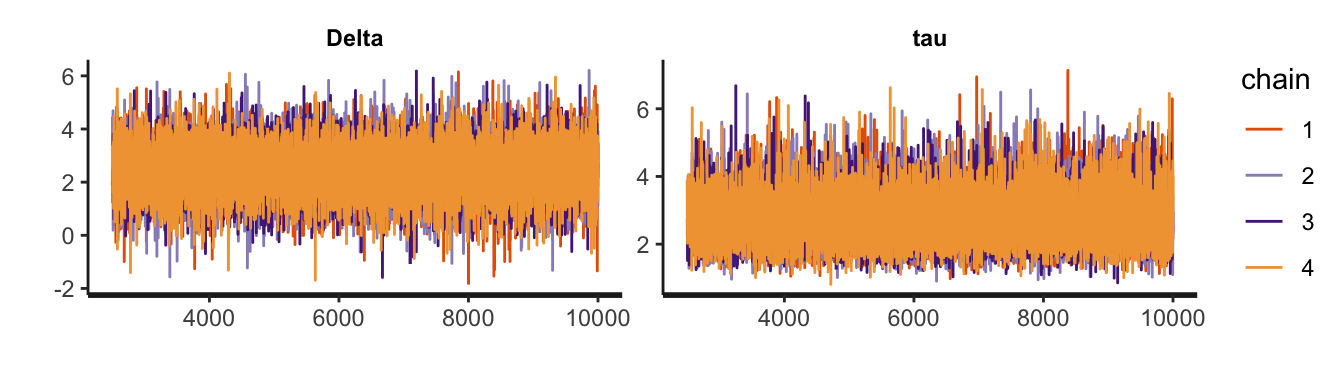
Look at the results
It is possible to look inspect the distribution of any or all parameters. In this case, I am particularly interested in the treatment effects at the study level, and overall. That is, the focus here is on \(\Delta\), \(\delta_k\), and \(\tau\).
pname <- c("delta", "Delta","tau")
print(fit, pars=pname, probs = c(0.05, 0.5, 0.95))## Inference for Stan model: model.
## 4 chains, each with iter=10000; warmup=2500; thin=1;
## post-warmup draws per chain=7500, total post-warmup draws=30000.
##
## mean se_mean sd 5% 50% 95% n_eff Rhat
## delta[1] 6.39 0.01 1.13 4.51 6.41 8.22 29562 1
## delta[2] -0.78 0.01 1.62 -3.45 -0.78 1.85 28188 1
## delta[3] -0.14 0.01 1.39 -2.37 -0.16 2.18 28909 1
## delta[4] 3.08 0.00 0.59 2.09 3.08 4.05 34277 1
## delta[5] -0.16 0.01 1.01 -1.77 -0.18 1.52 27491 1
## delta[6] 3.87 0.00 0.86 2.47 3.87 5.27 35079 1
## delta[7] 4.04 0.01 1.11 2.21 4.03 5.87 32913 1
## delta[8] 5.23 0.01 1.29 3.12 5.23 7.36 33503 1
## delta[9] 1.79 0.01 1.25 -0.27 1.78 3.82 30709 1
## delta[10] 1.38 0.01 1.12 -0.46 1.38 3.21 30522 1
## delta[11] 4.47 0.01 1.25 2.43 4.47 6.54 34573 1
## delta[12] 0.79 0.01 1.45 -1.60 0.80 3.16 33422 1
## Delta 2.48 0.00 0.89 1.01 2.50 3.89 31970 1
## tau 2.72 0.00 0.71 1.72 2.64 4.01 24118 1
##
## Samples were drawn using NUTS(diag_e) at Sat Jun 27 15:47:15 2020.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at
## convergence, Rhat=1).The forest plot is quite similar to the one based on the mixed effects model, though as predicted, the 95% CI is considerably wider:
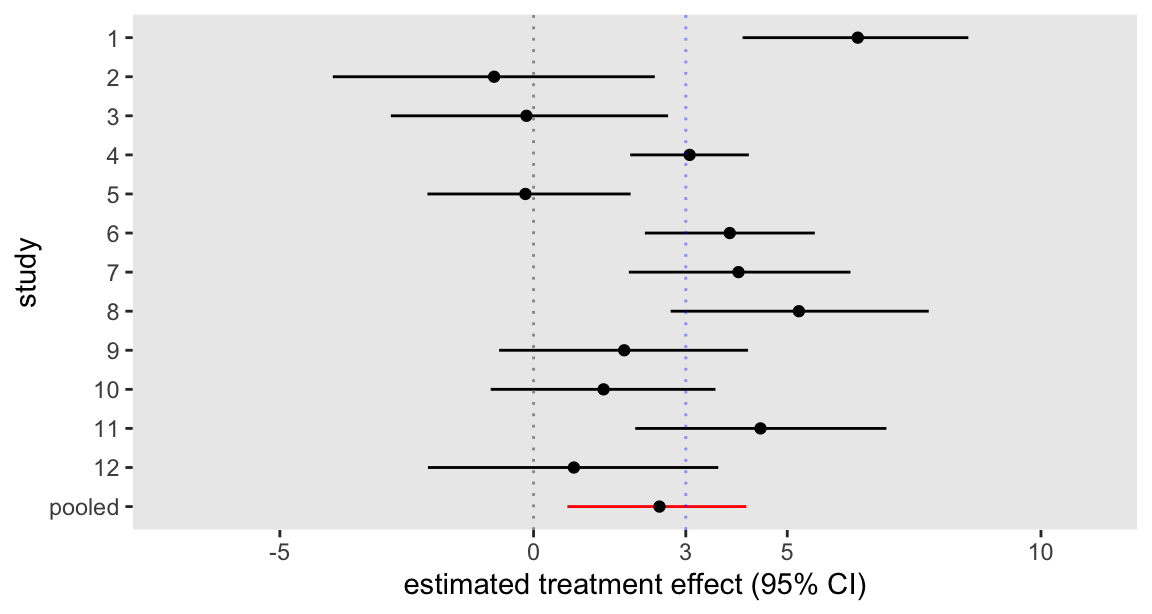
As a comparison, here is the plot from the mixed effects model estimated using the nlme package in the previous post. The bootstrapped estimates of uncertainty at the study level are quite close to the Bayesian measure of uncertainty; the difference really lies in the uncertainty around the global estimate.
