I am currently involved with an RCT that is struggling to recruit eligible patients (by no means an unusual problem), increasing the risk that findings might be inconclusive. A possible solution to this conundrum is to find similar, ongoing trials with the aim of pooling data in a single analysis, to conduct a meta-analysis of sorts.
In an ideal world, this theoretical collection of sites would have joined forces to develop a single study protocol, but often there is no structure or funding mechanism to make that happen. However, this group of studies may be similar enough - based on the target patient population, study inclusion and exclusion criteria, therapy protocols, comparison or control condition, randomization scheme, and outcome measurement - that it might be reasonable to estimate a single treatment effect and some measure of uncertainty.
This pooling approach would effectively be a prospective meta-analysis using individual participant data. The goal is to estimate a single treatment effect for this intervention or therapy that has been evaluated by different groups under varying research conditions, with possibly different treatment effects in each study.
To explore how all of this works, I generated some data and fit some models. As usual I thought the code would be more useful sitting on this blog rather than hidden away on some secure server.
The model
In this simulation, I am using a generic continuous outcome , for individual who is participating in study . The individual outcome is a function of the study itself and whether that individual received the experimental therapy ( for patients in the experimental arm):
is the intercept for study , or the average outcome for patients in study in the control arm. is the treatment effect in study and can be decomposed into a common treatment effect across all studies and a study-specific effect . is often assumed to be normally distributed, . An individual effect, is also assumed to be normally distributed, . Note that the variance of individual effects might differ across studies; that is, in some studies patients may be more similar to each other than in other studies.
The simulation assumptions
Before starting - here are the necessary libraries in case you want to follow along:
library(simstudy)
library(parallel)
library(nlme)
library(data.table)In these simulations, there are 12 studies, each enrolling a different number of patients. There are a set of smaller studies, moderately sized studies, and larger studies. We are not really interested in the variability of the intercepts (’s), but we generate based on a normal distribution . The overall treatment effect is set at , and the study-specific effects are distributed as . We use a gamma distribution to create the study-specific within study variation : the average within-study variance is , and will range between and (the variance of the variances is ). The study-specific data are generated using these assumptions:
defS <- defData(varname = "a.k", formula = 3, variance = 2, id = "study")
defS <- defData(defS, varname = "d.0", formula = 3, dist = "nonrandom")
defS <- defData(defS, varname = "v.k", formula = 0, variance = 6, dist= "normal")
defS <- defData(defS, varname = "s2.k", formula = 16, variance = .2, dist = "gamma")
defS <- defData(defS, varname = "size.study", formula = ".3;.5;.2", dist = "categorical")
defS <- defData(defS, varname = "n.study",
formula = "(size.study==1) * 20 + (size.study==2) * 40 + (size.study==3) * 60",
dist = "poisson")The individual outcomes are generated based on the model specified above:
defI <- defDataAdd(varname = "y", formula = "a.k + x * (d.0 + v.k)", variance = "s2.k")Data generation
First, we generate the study level data:
RNGkind(kind = "L'Ecuyer-CMRG")
set.seed(12764)
ds <- genData(12, defS)
ds## study a.k d.0 v.k s2.k size.study n.study
## 1: 1 2.51 3 2.7437 5.25 2 30
## 2: 2 1.51 3 -4.8894 30.48 2 37
## 3: 3 1.62 3 -4.1762 15.06 1 22
## 4: 4 3.34 3 0.2494 3.26 2 44
## 5: 5 2.34 3 -2.9078 5.59 1 15
## 6: 6 1.70 3 1.3498 7.42 2 44
## 7: 7 4.17 3 -0.4135 14.58 2 45
## 8: 8 2.14 3 0.7826 25.78 2 44
## 9: 9 2.54 3 -1.1197 15.72 1 28
## 10: 10 3.10 3 -2.1275 10.00 1 24
## 11: 11 2.62 3 -0.0812 32.76 2 40
## 12: 12 1.17 3 -0.5745 30.94 2 49And then we generate individuals within each study, assign treatment, and add the outcome:
dc <- genCluster(ds, "study", "n.study", "id", )
dc <- trtAssign(dc, strata = "study", grpName = "x")
dc <- addColumns(defI, dc)The observed data set obviously does not include any underlying study data parameters. The figure based on this data set shows the individual-level outcomes by treatment arm for each of the 12 studies. The study-specific treatment effects and differences in within-study variation are readily apparent.
d.obs <- dc[, .(study, id, x, y)]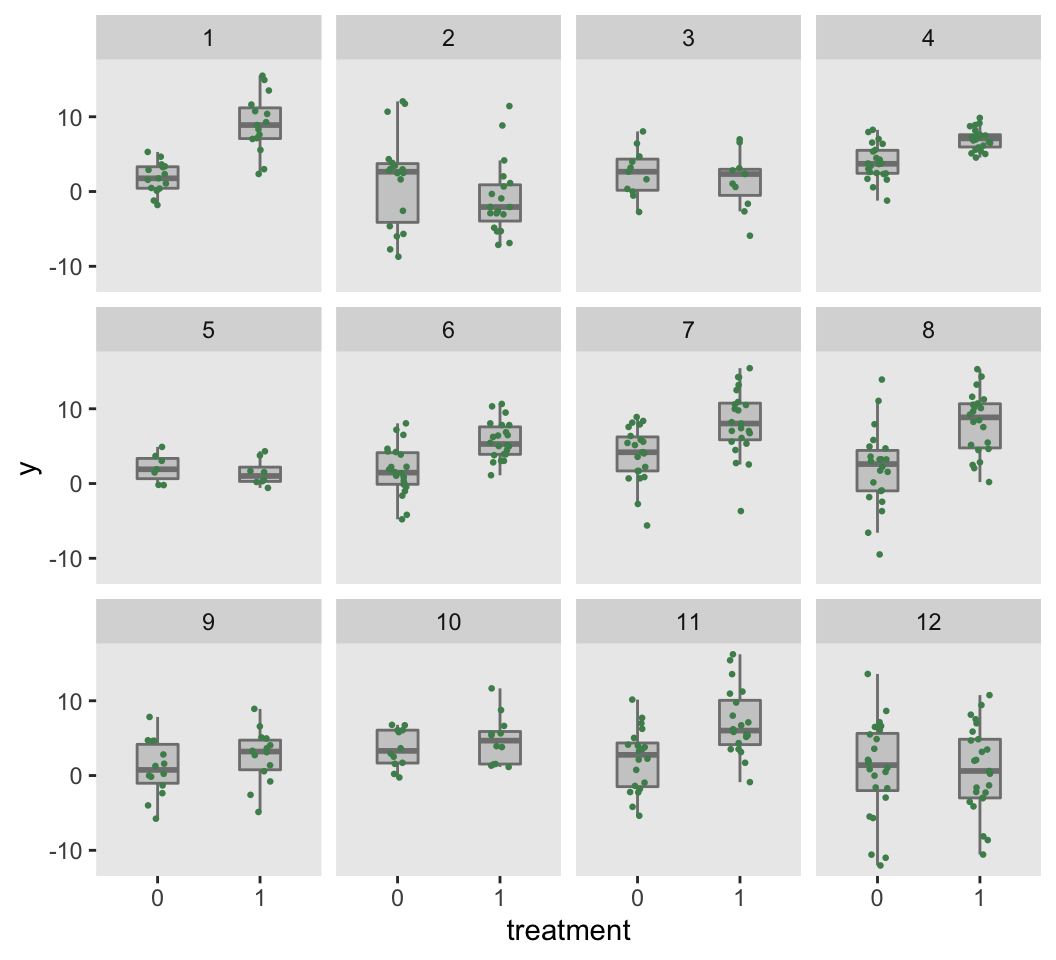
Initial estimates
If each study went ahead and analyzed its own data set separately, the emerging picture would be a bit confusing. We would have 12 different estimates, some concluding that the treatment is effective, and others not able to draw that conclusion. A plot of the 12 model estimates along with the 95% confidence intervals highlights the muddled picture. For additional reference, I’ve added points that represent the true (and unknown) study effects in blue, including a blue line at the value of the overall treatment effect.
lm.ind <- function(z, dx) {
fit <- lm(y~x, data = dx)
data.table(z, coef(fit)["x"], confint(fit, "x"))
}
res <- lapply(1:d.obs[, length(unique(study))], function(z) lm.ind(z, d.obs[study == z]))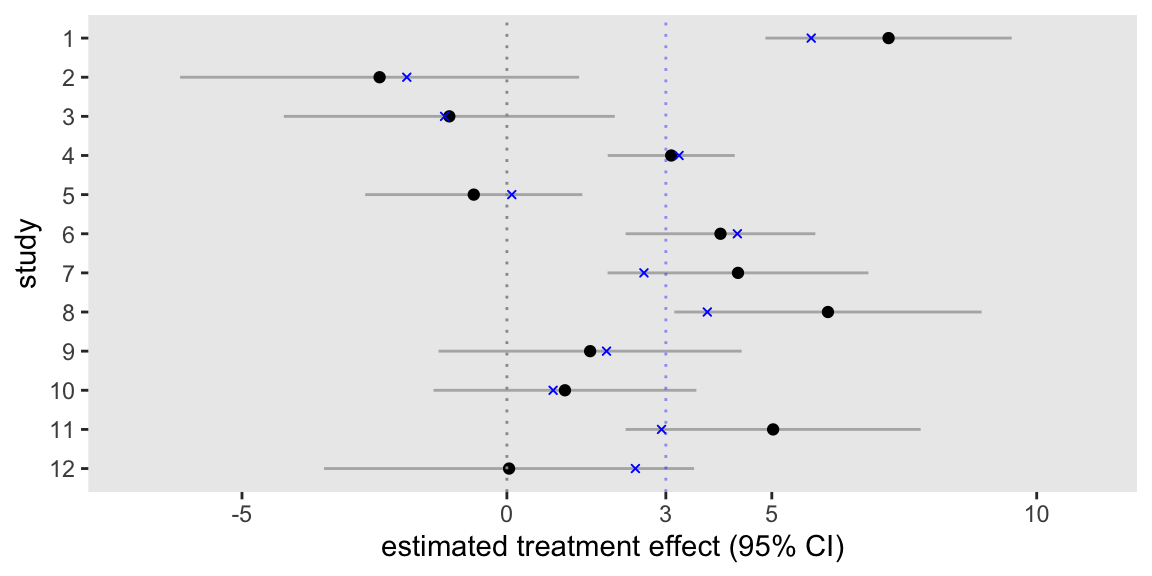
The meta-analysis
The meta-analysis is an attempt to pool the findings from all the studies to try to draw an overall conclusion. Traditionally, meta-analysis has been conducted using only the summary information from each study - effect size estimates, standard errors, and sample sizes. More recently, researchers have started to use individual-level data to estimate an overall effect. There are advantages to this added level of detail, particularly in enhancing the ability to model patient-level and study-level characteristics that might influence the effect size; these adjustments could help reduce the variance of the effect size estimates.
There are packages in R specifically designed to conduct meta-analysis, but I am doing it “manually” through the use of the nlme package, which estimates mixed-effects model that mimics the underlying data process. (In a subsequent post, I will do the same thing using a Bayesian model implement using rstan.) I opted for nlme over the lme4 package, because the former can accommodate the possibility of different within-study variation.
The model fit here includes a study specific (fixed) intercept, an overall treatment effect, and a study-specific treatment effect. And, as I just mentioned, the within-study variation is accommodated:
lmefit <- lme(y ~ factor(study) + x - 1,
random = ~ x - 1 | study,
weights = varIdent(form = ~ 1 | study),
data = d.obs, method = 'REML'
)The model estimate for the overall treatment effect is 2.5, just under but close to the true value of 3.0:
round(coef(summary(lmefit))["x",], 3)## Warning in pt(-abs(tVal), fDF): NaNs produced## Value Std.Error DF t-value p-value
## 2.481 0.851 410.000 2.915 0.004Bootstrapping uncertainty
Every meta-analysis I’ve seen includes a forest plot that shows the individual study estimates along with the global estimate of primary interest. In my version of this plot, I wanted to show the estimated study-level effects from the model () along with 95% confidence intervals. The model fit does not provide a variance estimate for each study-level treatment effect, so I have estimated the standard error using bootstrap methods. I repeatedly sample from the observed data (sampling stratified by study and treatment arm) and estimate the same fixed effects model. For each iteration, I keep the estimated study-specific treatment effect as well as the estimated pooled effect:
bootest <- function() {
bootid <- d.obs[, .(id = sample(id, .N, replace = TRUE)), keyby = .(study, x)][, .(id)]
dboot <- merge(bootid, d.obs, by = "id")
bootfit <- tryCatch(
{ lme(y ~ factor(study) + x - 1,
random = ~ x - 1 | study,
weights = varIdent(form = ~ 1 | study),
data = dboot, method = 'REML')
},
error = function(e) {
return("error")
},
warn = function(w) {
return("warning")
}
)
if (class(bootfit) == "lme") {
return(data.table(t(random.effects(bootfit) + fixed.effects(bootfit)["x"]),
pooled = fixed.effects(bootfit)["x"]))
}
}
res <- mclapply(1:3000, function(x) bootest(), mc.cores = 4)
res <- rbindlist(res)The next plot shows the individual study estimates based on the pooled analysis along with the overall estimate in red, allowing us to bring a little clarity to what was an admittedly confusing picture. We might conclude from these findings that the intervention appears to be effective.
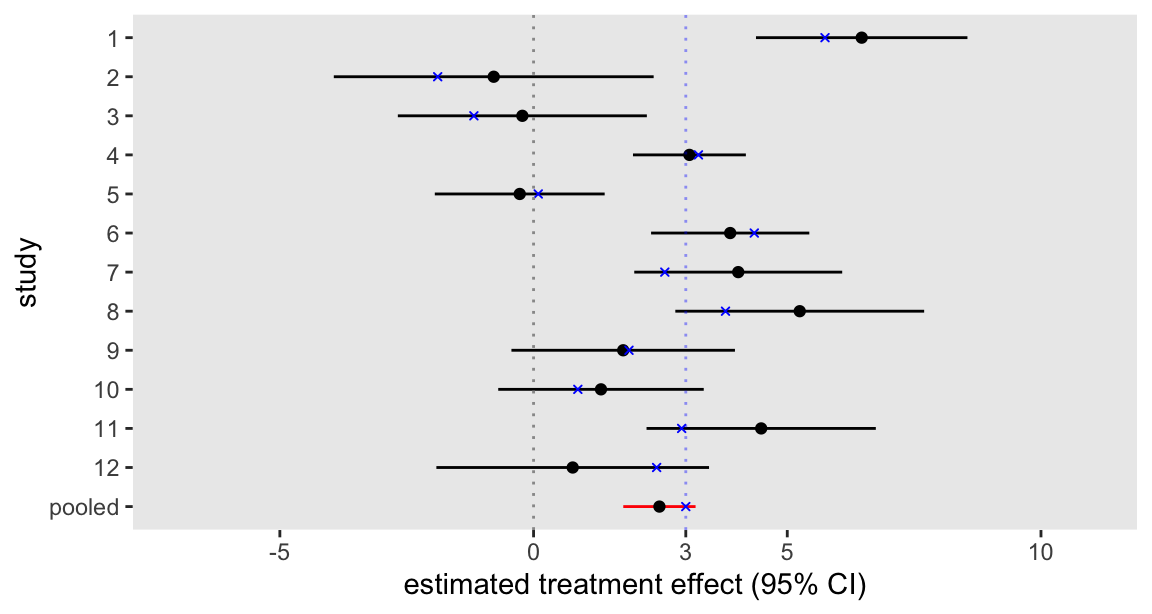
As an aside, it is interesting to compare the two forest plot figures in the post, because it is apparent that the point estimates for the individual studies in the second plot are “pulled” closer to the overall average. This is the direct result of the mixed effects model that imposes a structure in the variation of effect sizes across the 12 studies. In contrast, the initial plot shows individual effect sizes that were independently estimated without any such constraint or structure. Pooling across groups or clusters generally has an attenuating effect on estimates.