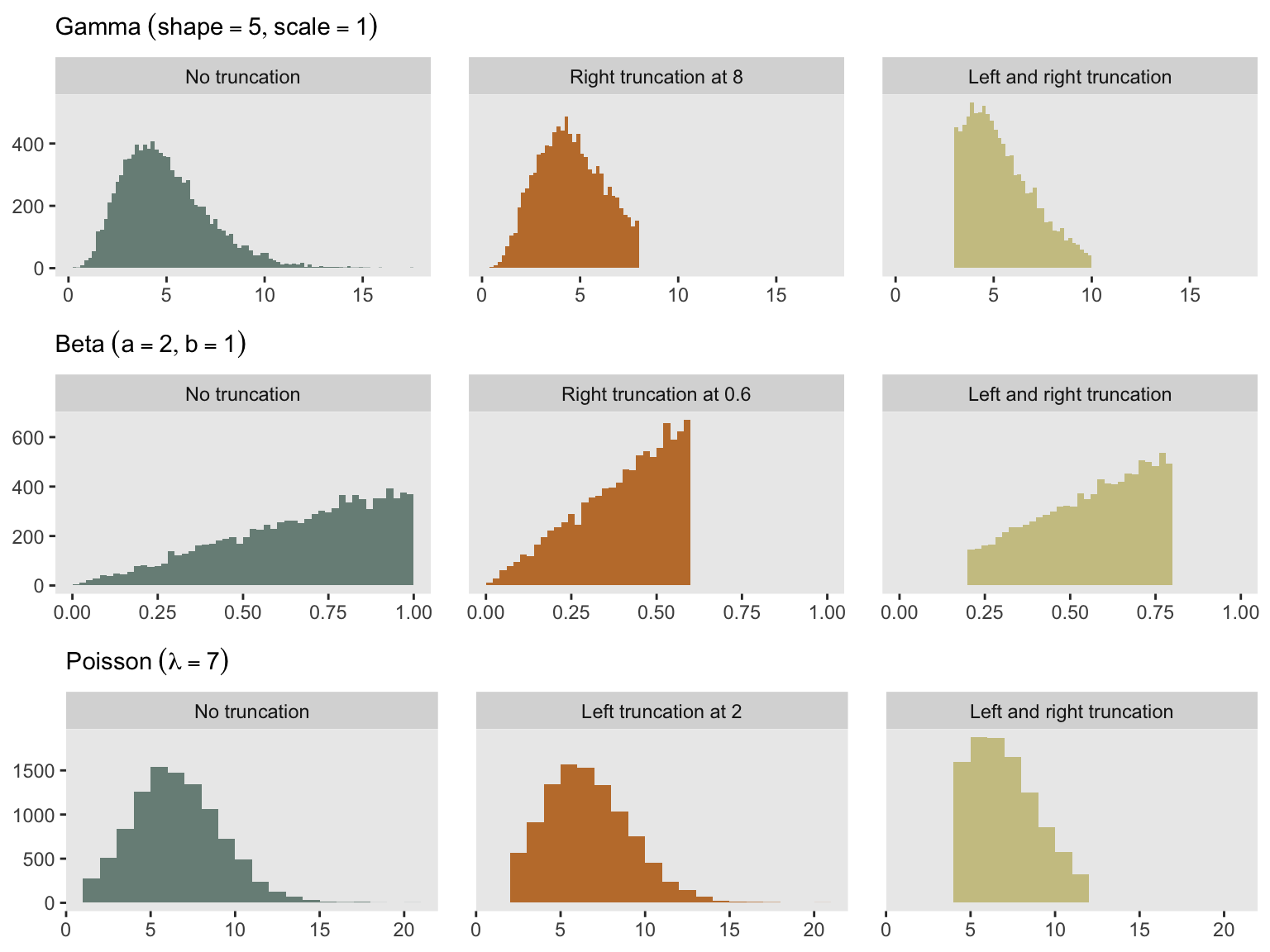
A researcher reached out to me the other day to see if the simstudy package provides a quick and easy way to generate data from a truncated distribution. Other than the noZeroPoisson distribution option (which is a very specific truncated distribution), there is no way to do this directly. You can always generate data from the full distribution and toss out the observations that fall outside of the truncation range, but this is not exactly efficient, and in practice can get a little messy. I’ve actually had it in the back of my mind to add something like this to simstudy, but have hesitated because it might mean changing (or at least adding to) the defData table structure.
However, it may be time to go for it. The process and coding are actually relatively straightforward, so there is no real reason not to. I was developing a simple prototype for several probability distributions (though the concept can easily be applied to any distribution where the cumulative distribution function, or CDF, is readily accessible), and am sharing here in case you need to do this before it is available in the package, or if you just want to implement yourself.
What is a truncated distribution?
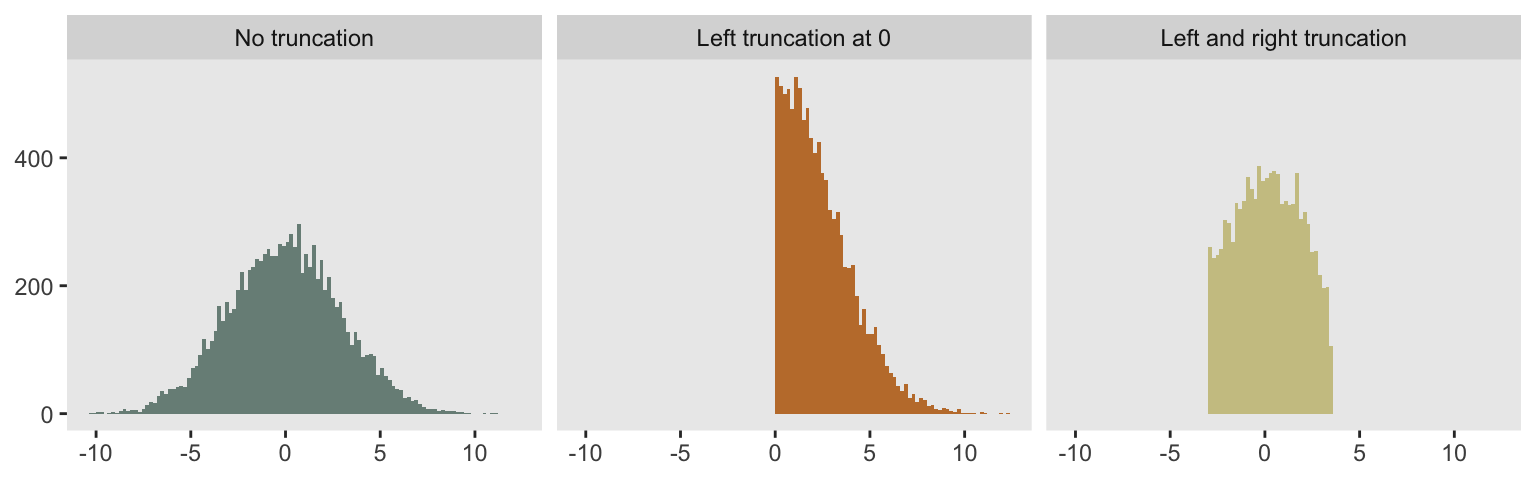
A truncated probability distribution is one derived from limiting the domain of an existing distribution. A picture is worth a thousand words. On the left, we have a histogram for 10,000 observations drawn from a full (non-truncated) Gaussian or normal distribution with mean 0 and standard deviation 3. In the middle, the histogram represents data drawn from the positive portion of the same distribution (i.e. is truncated at the left by 0). And on the far right, the truncation is defined by the boundaries \((-3, 3.5)\):
Leveraging the uniform distribution and a CDF
A while back, I described a copula approach to generating correlated data from different distributions (ultimately implemented in functions genCorGen and addCorGen). I wrote about combining a draw from a uniform distribution with the CDF of any target distribution to facilitate random number generation from the target generation. This is an approach that works well for truncated distributions also, where the truncated distribution is the target.
Again - visuals help to explain how this works. To start, here are several CDFs of normal distributions with different means and variances:
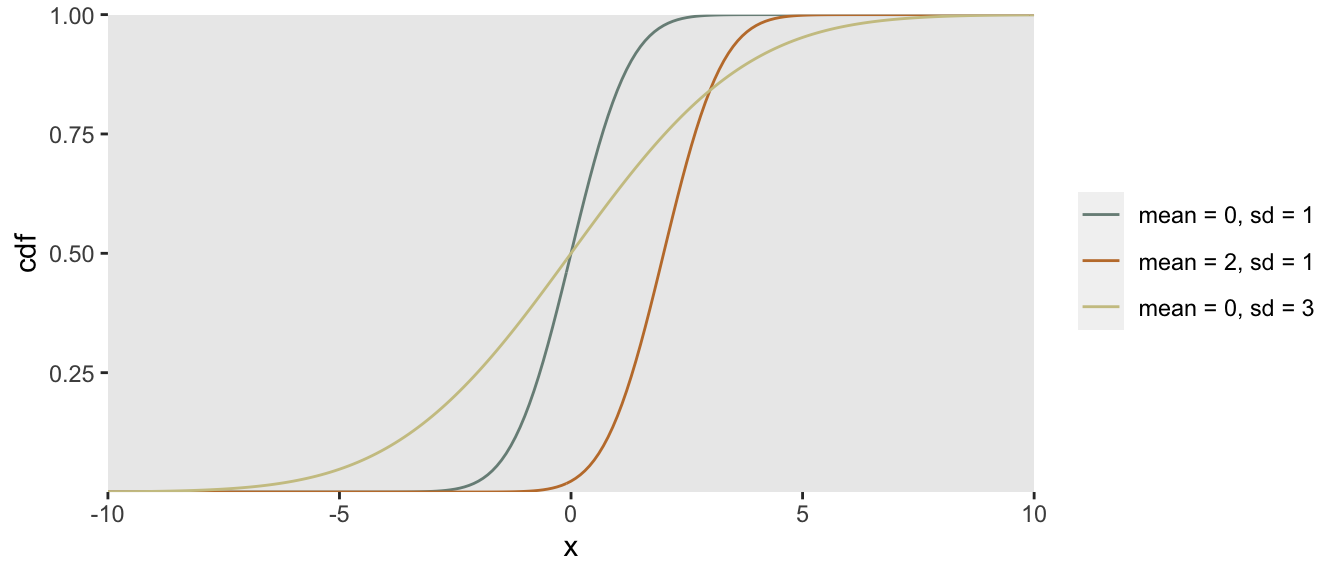
The CDF of a distribution (usually written as \(F(x)\)) effectively defines that distribution: \(F(x) = P(X \le x)\). Since probabilities by definition range from \(0\) to \(1\), we know that \(F(x)\) also ranges from \(0\) to \(1\). It is also the case, that \(F(x)\) is monotonically increasing (or at least non-decreasing) from \(0\) to \(1\).
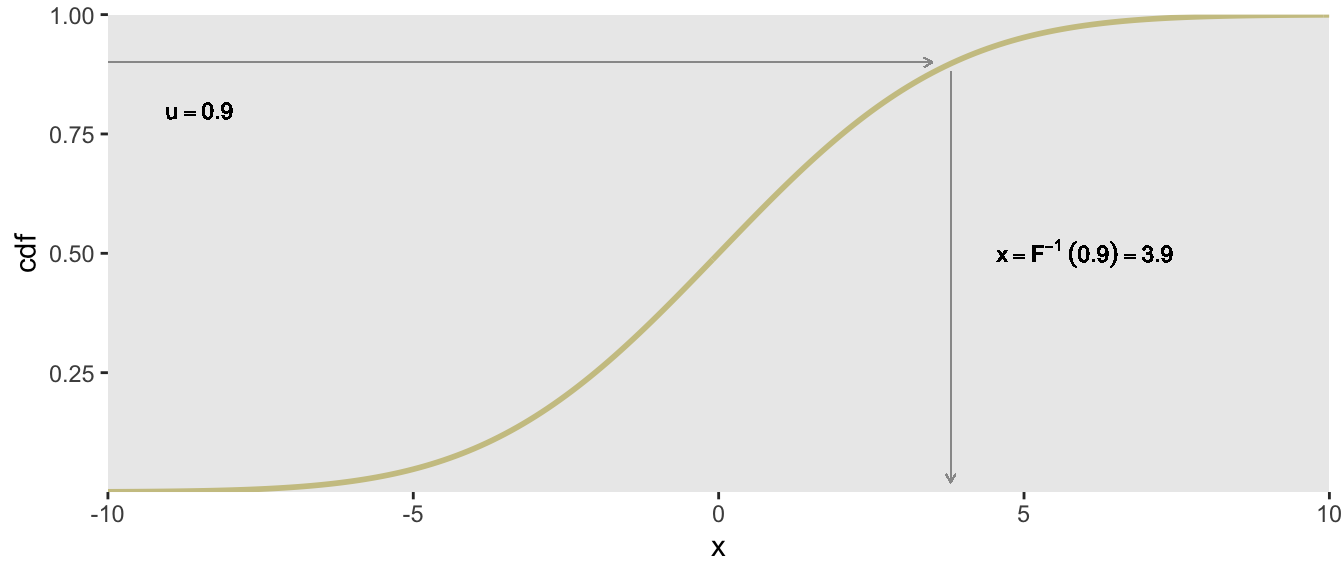
Let’s say we want to generate a draw from \(N(\mu =0, \sigma = 3)\) using the the CDF. We can first generate a draw from \(u = Uniform(0,1)\). We then treat \(u\) as a value of the CDF, and map it back \(x\) to get our draw from the target distribution. So, \(x = F^{-1}(u)\). In R, the CDF for the normal distribution can be determined using the qnorm function, where the first argument is a probability value between \(0\) and \(1\). This would be the R code to generate a single draw from \(N(0, 3)\) using a random draw from \(Uniform(0, 1)\):
(u <- runif(1))## [1] 0.9qnorm(u, mean = 0, sd = 3)## [1] 3.9This is how \(u = 0.9\) relates to the draw of \(x=3.9\):
To generate a random sample of 10,000 draws from \(N(0, 3)\), this process is replicated 10,000 times:
library(ggplot2)
u <- runif(10000)
x <- qnorm(u, mean = 0, sd = 3)
ggplot(data = data.frame(x), aes(x = x)) +
geom_histogram(fill = "#CCC591", alpha = 1, binwidth = .2, boundary = 0) +
theme(panel.grid = element_blank(),
axis.title = element_blank())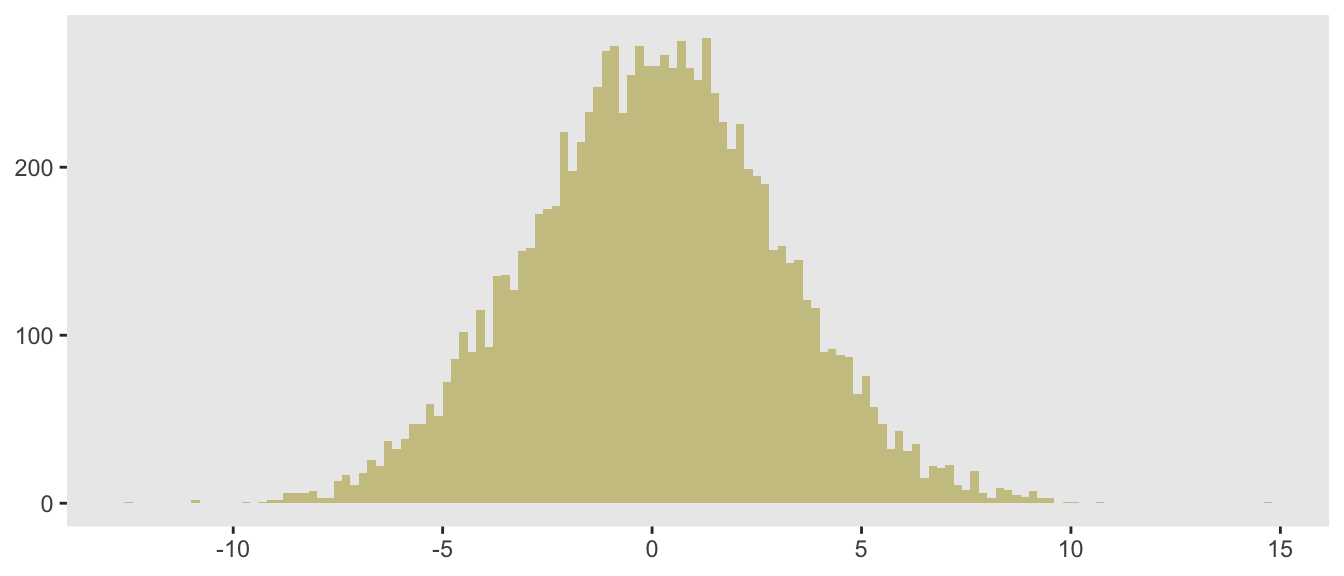
Extending the inverse process to generate truncation
Let’s say we are only interested in generating data from the middle portion of the \(N(0,3)\) distribution, between \(a\) and \(b\). The trick is to use the corresponding CDF values, \(F(a)\) and \(F(b)\) as the basis of the randomization.
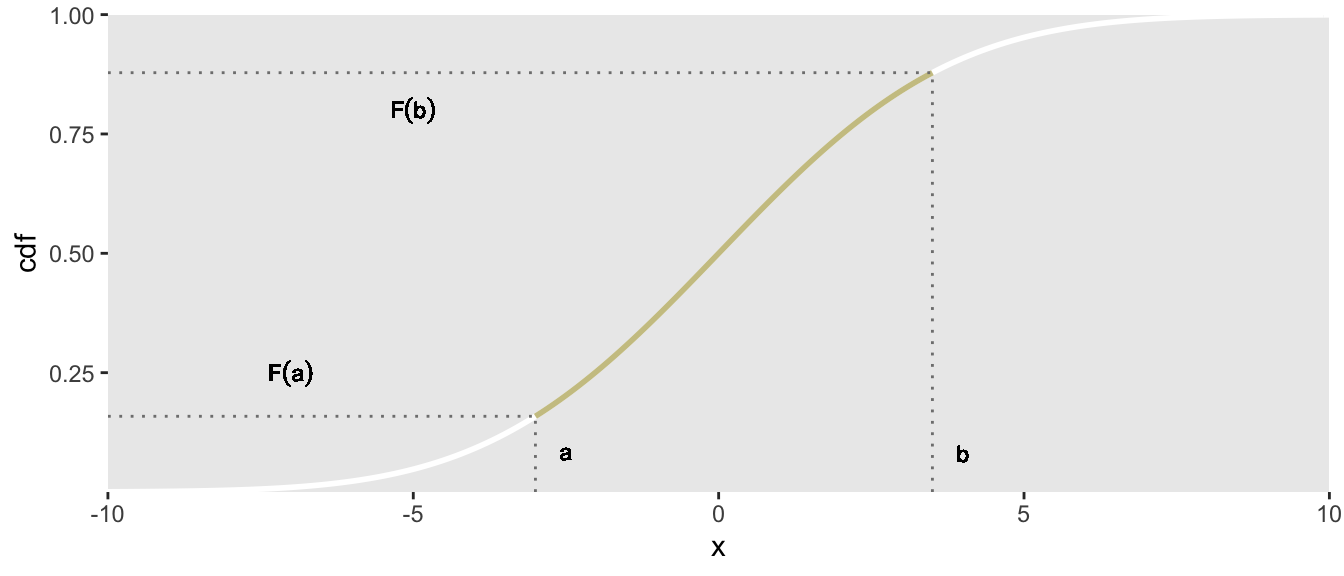
To generate data within the constraints \(a\) and \(b\), all we would need to do is generate a value from the uniform distribution with minimum equal to \(F(a)\) and maximum \(F(b)\). We then conduct the mapping as we did before when drawing from the full distribution. By constraining \(u\) to be between \(F(a)\) and \(F(b)\), we force the values of the target distribution to lie between \(a\) and \(b\).
Now, we are ready to create a simple function rnormt that implements this: The pnorm function provides the CDF at a particular value:
rnormt <- function(n, range, mu, s = 1) {
# range is a vector of two values
F.a <- pnorm(min(range), mean = mu, sd = s)
F.b <- pnorm(max(range), mean = mu, sd = s)
u <- runif(n, min = F.a, max = F.b)
qnorm(u, mean = mu, sd = s)
}Here, I am generating the data plotted above, showing the code this time around.
library(data.table)
library(simstudy)
library(paletteer)
defC <- defCondition(condition= "tt == 1",
formula = "rnormt(10000, c(-Inf, Inf), mu = 0, s = 3)")
defC <- defCondition(defC, "tt == 2",
formula = "rnormt(10000, c(0, Inf), mu = 0, s = 3)")
defC <- defCondition(defC, "tt == 3",
formula = "rnormt(10000, c(-3, 3.5), mu = 0, s = 3)")
dd <- genData(30000)
dd <- trtAssign(dd, nTrt = 3, grpName = "tt")
dd <- addCondition(defC, dd, "x")
dd[, tt := factor(tt,
labels = c("No truncation", "Left truncation at 0", "Left and right truncation"))]
ggplot(data = dd, aes(x = x, group = tt)) +
geom_histogram(aes(fill = tt), alpha = 1, binwidth = .2, boundary = 0) +
facet_grid(~tt) +
theme(panel.grid = element_blank(),
axis.title = element_blank(),
legend.position = "none") +
scale_fill_paletteer_d("wesanderson::Moonrise2")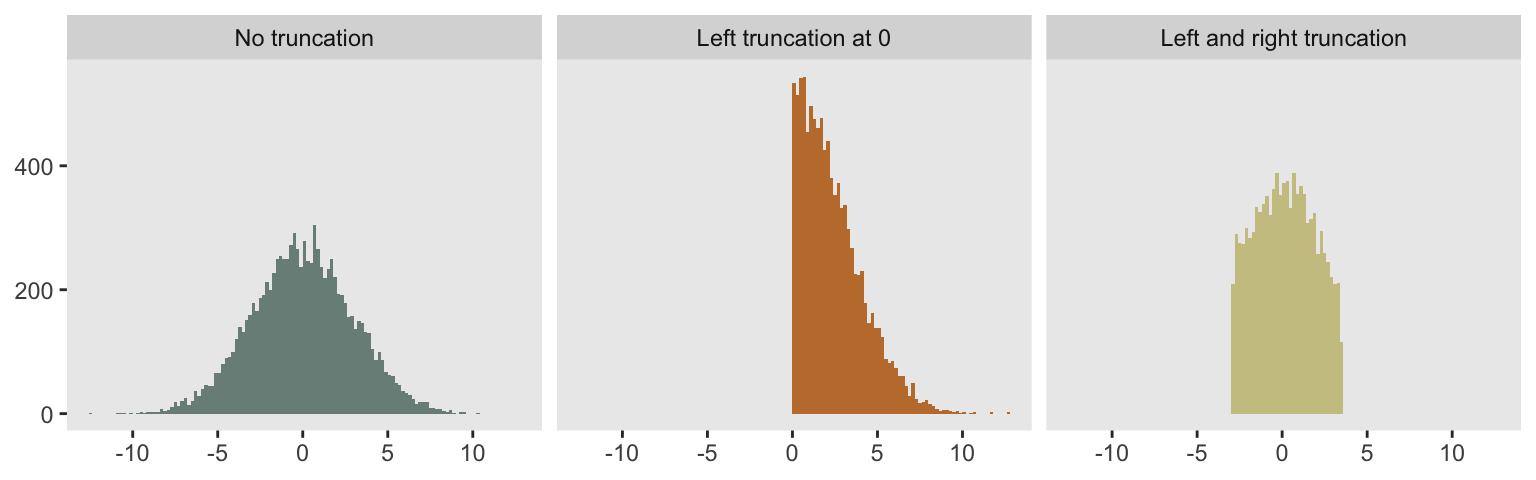
Going beyond the normal distribution
With this simple approach, it is possible to generate a truncated distribution using any distribution available in R. Here is another example that allows us to generate truncated data from a gamma distribution:
rgammat <- function(n, range, shape, scale = 1) {
F.a <- pgamma(min(range), shape = shape, scale = scale)
F.b <- pgamma(max(range), shape = shape, scale = scale)
u <- runif(n, min = F.a, max = F.b)
qgamma(u, shape = shape, scale = scale)
}To conclude, here is a plot of gamma-based distributions using rgammat. And I’ve added similar plots for beta and Poisson distributions - I’ll leave it to you to write the functions. But, if you don’t want to do that, simstudy will be updated at some point soon to help you out.
