As a biostatistician, I like to be involved in the design of a study as early as possible. I always like to say that I hope one of the first conversations an investigator has is with me, so that I can help clarify the research questions before getting into the design questions related to measurement, unit of randomization, and sample size. In the worst case scenario - and this actually doesn’t happen to me any more - a researcher would approach me after everything is done except the analysis. (I guess this is the appropriate time to pull out the quote made by the famous statistician Ronald Fisher: “To consult the statistician after an experiment is finished is often merely to ask him to conduct a post-mortem examination. He can perhaps say what the experiment died of.”)
In these times, when researchers are scrambling to improve care for patients the Covid-19, there isn’t often time for those early conversations, or they are happening with many different people. Recently, I’ve been asked to help figure out what the sample size requirements are for four or five studies involving promising therapies for Covid-19 patients at various stages of the disease. In most cases, randomization is at the patient, so power/sample size calculations are much simpler. In other situations, cluster randomization at the unit or hospital floor level is being considered, so the sample size estimates are a little more involved.
There are analytic/formula solutions for sample size estimates in non-clustered randomization. And if the outcome is continuous, adjustments can be made using an estimate of the design effect, which I wrote about recently. When the outcome is binary, or the number of clusters is small, or the cluster sizes themselves are small, I feel more comfortable using simulation methods. Indeed, the simstudy package grew out of my work to facilitate data generation for this very reason.
My intention here is to provide code to help others in case they want to conduct these relatively simple power analyses. One of the proposed studies expected to have a large number of small-sized clusters, so that is what I’ll simulate here.
The data generation process
To estimate power under a range of scenarios, I’ve written two functions to define the data generation process, one to generate the data, and a final one to generate a single data set and estimate the parameters of a mixed effects model.
data definitions
The variance of the cluster-level random effect is based on a conversion of the intra-cluster correlation (ICC) to the logistic scale, which is done through a call to the function iccRE. The definition of the outcome is based on this random effect plus a log odds-ratio that is derived from the control proportion and the assumed percent change:
library(simstudy)
library(lme4)
defRE <- function(icc, dist = "binary", varW = NULL) {
setVar <- iccRE(ICC = icc, dist = dist, varWithin = varW)
def <- defData(varname = "a", formula = 0, variance = setVar, id = "cluster")
return(def)
}
defBinOut <- function(p1, pctdelta) {
p2 <- (1 - pctdelta) * p1
int <- round(log( p1/(1-p1) ), 4)
effect <- round(log( (p2/(1-p2)) / (p1/(1-p1) )), 4)
formula <- genFormula( c(int, effect, 1), c("rx","a") )
def <- defDataAdd(varname = "y", formula = formula, dist = "binary",
link = "logit")
return(def)
}data generation
The data generation follows from the data definitions. First, cluster-level data are generated (along with treatment assignment), and then the individual patient level data.
genDataSet <- function(nclust, clustsize, re.def, out.def) {
dClust <- genData(nclust, re.def)
dClust <- trtAssign(dClust, grpName = "rx")
dPat <- genCluster(dtClust = dClust, cLevelVar = "cluster",
numIndsVar = clustsize, level1ID = "id")
dPat <- addColumns(out.def, dPat)
return(dPat)
}model estimation
The p-values used for the power calculation are estimated using glmer of the lme4 package, a generalized mixed effects model. (If the outcome were continuous, we would use lmer instead.) Unfortunately, this can be relatively resource-intensive, so the repeated estimations over a wide range of scenarios can be rather time consuming.
One way to speed things up is eliminate a step in the glmer algorithm to that takes considerable time, but has the side effect of excluding information about whether or not the model estimation has converged. Convergence can be a particular problem if variation across clusters is low, as when the ICC is low. The function below keeps track of whether an iteration has converged (but only if fast is set to FALSE). One might want to explore how frequently there is a failure to converge before turning on the fast flag.
This function returns the convergence status, the estimate of the random effects variance, and the effect parameter estimate, standard error, and p-value.
genBinEsts <- function(nclust, clustsize, re.def, out.def, fast = FALSE) {
dP <- genDataSet(nclust, clustsize, re.def, out.def)
mod.re <- glmer(y ~ rx + (1|cluster), data = dP, family = binomial,
control = glmerControl( optimizer = "bobyqa", calc.derivs = !(fast) ))
convStatus <- as.numeric(length(summary(mod.re)$optinfo$conv$lme4))
res <- data.table(convStatus, re = VarCorr(mod.re)$cluster,
t(coef(summary(mod.re))["rx",]))
return(res)
}Single data set
Here is an example setting the ICC at 0.025, the control proportion at 40%, and an effect size that translates to a 30% reduction (so that the treatment proportion will be 28%).
(defa <- defRE(icc = 0.025))## varname formula variance dist link
## 1: a 0 0.0844 normal identity(defy <- defBinOut(0.40, 0.30))## varname formula variance dist link
## 1: y -0.4055 + -0.539 * rx + 1 * a 0 binary logitAnd when we generate a single data set and estimate the parameters by calling the last function:
RNGkind("L'Ecuyer-CMRG")
set.seed(2711)
genBinEsts(40, 10, defa, defy)## convStatus re.(Intercept) Estimate Std. Error z value Pr(>|z|)
## 1: 0 0.284 -0.625 0.279 -2.24 0.0249Estimating power
Everything is set up now to estimate power with repeated calls to this group of functions. This process can be done using the mclapply function in the parallel package, as I illustrated in earlier post. Here, I am showing a for loop implementation.
The variables ICC, SS, nClust, ctlPROB, and pctDELTA are vectors containing all the possible scenarios for which power will be estimated. In this case, power will be based on 1000 iterations under set of assumptions.
library(parallel)
nIters <- 1000
results <- NULL
for (icc in ICC) {
for (ss in SS) {
for (nclust in nCLUST) {
for (p1 in ctlPROB) {
for (pdelta in pctDELTA) {
clustsize <- ss %/% nclust
p2 <- p1 * (1 - pdelta)
defa <- defRE(icc)
defy <- defBinOut(p1, pdelta)
res <- rbindlist(mclapply(1:nIters,
function(x) genBinEsts(nclust, clustsize, defa, defy)))
dres <- data.table(icc, ss, nclust, clustsize, p1, p2, pdelta,
converged = res[, mean(convStatus == 0)],
p.conv = res[convStatus == 0, mean(`Pr(>|z|)` < 0.05)],
p.all = res[convStatus != 2, mean(`Pr(>|z|)` < 0.05)])
print(dres)
results <- rbind(results, dres)
}
}
}
}
}The first set of simulations evaluated power at a range of ICC’s, sample sizes, and effect sizes (in terms of percentage reduction). The number of clusters was fixed at 40, so the cluster size increased along with sample size. The probability of an event for a patient in the control group was also fixed at 10%.
ICC <- seq(0.025, .10, 0.025)
SS <- seq(200, 1600, 200)
pctDELTA <- c(.2, .3, .4, .5, .6)
nCLUST <- 40
ctlPROB <- 0.10The plot shows that at total sample sizes less 800, we would only be able detect effect sizes of 60% when the control proportion is 10%.
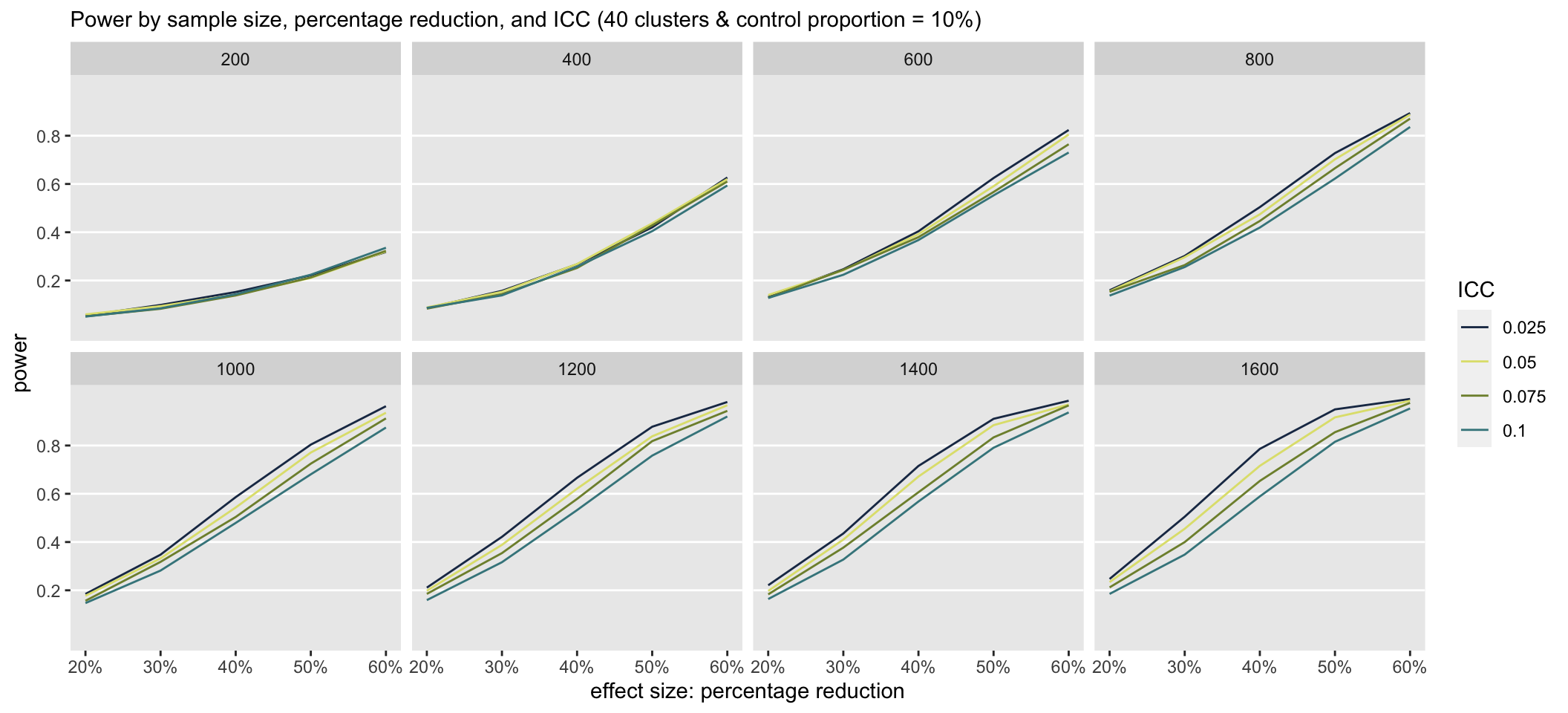
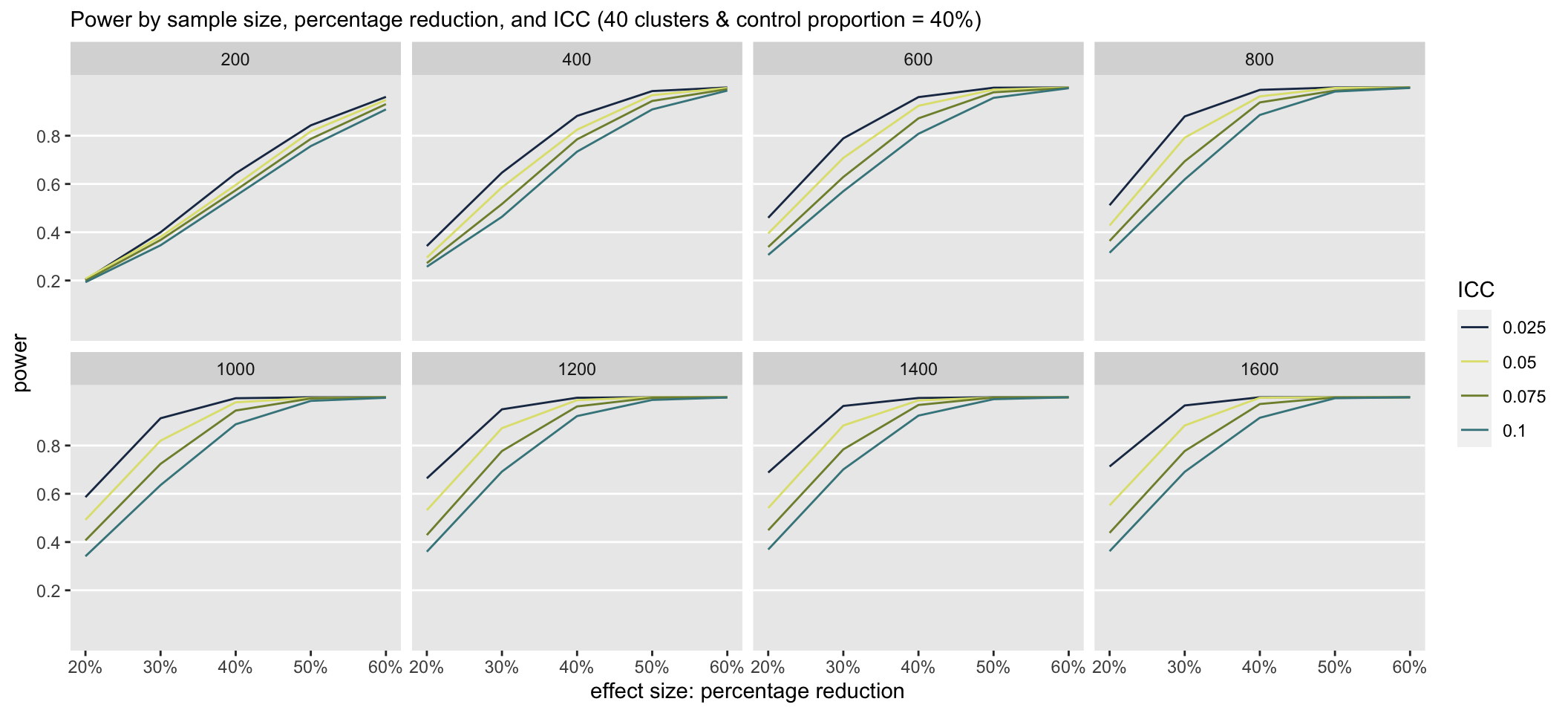
When the control proportion is at 40%, there is clearly a much higher probability that the study will detect an effect even at the smaller sample sizes. Under these scenarios, the ICC has a much greater impact on power than when the control proportion is much lower.
Other properties of the design
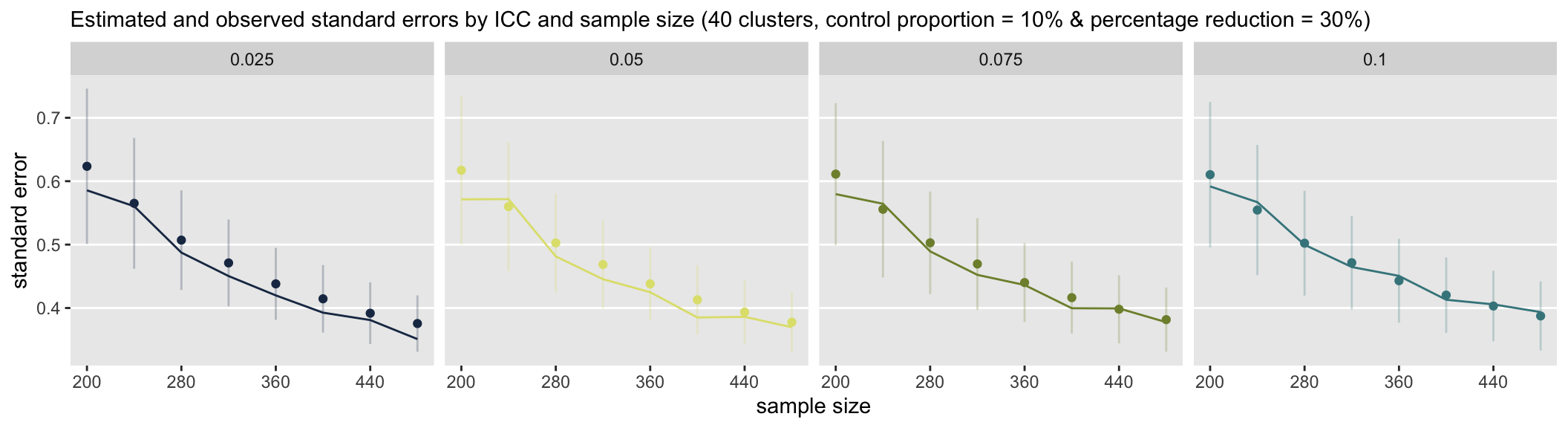
Of course, power is only one concern of many. For example, we may need to understand how a study’s design relates to bias and variance. In this case, I wondered how well the standard error estimates would compare to observed standard errors, particularly when the cluster sizes were on the lower end. Here are two plots comparing the two.
The lines represent the observed standard errors (the standard deviation of the measure of effect, or the parameter representing the log odds-ratio) at each sample size (assuming 40 clusters and an effect size of 30% reduction.) The points are the average estimate of the standard error with error bars that reflect 1 standard deviation.
In the first set scenarios, the control probability is set at 10%. For all ICCs except perhaps 0.10, it appears that the standard error estimates are, on average, too large, though there is quite a bit of variability. The over-estimation declines as between cluster variance increases.
In the second set of scenarios, where the control probability is at 40%, there is less variation in the standard error estimates (as reflected in the shorter length error bars), and there appears to be a slight underestimate of variation, particularly with the larger ICCs.
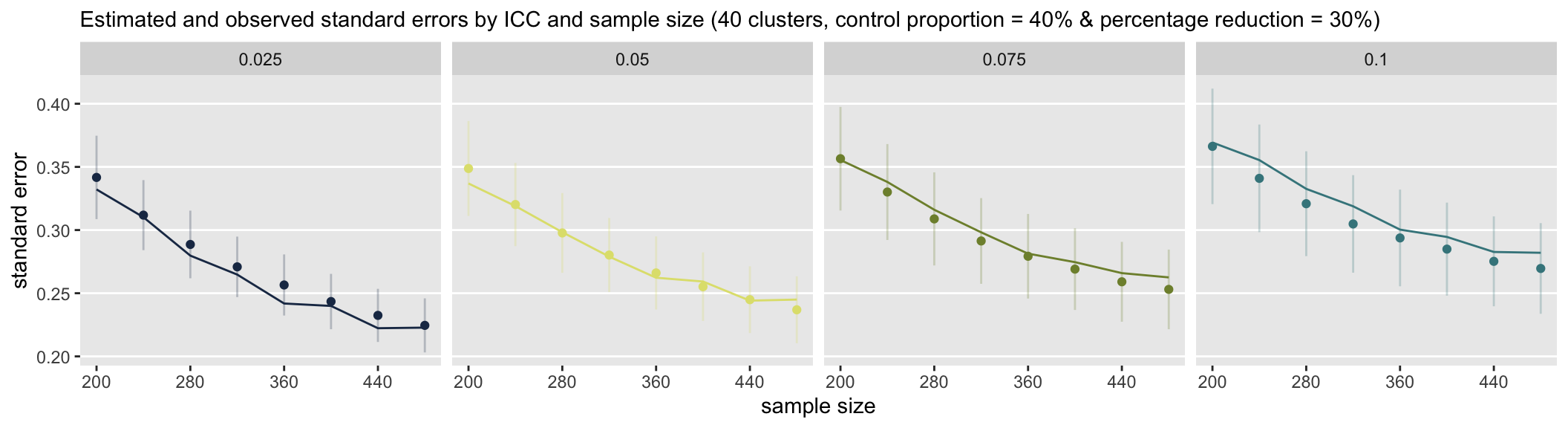
I have only scratched the surface here in terms of the scenarios that can be investigated. In addition there are other measurements to consider. Clearly, it would be useful to know if these observed biases in the standard error estimates disappear with larger cluster sizes, or how the number of clusters relates to this bias. And, I didn’t even look at the whether effect size estimates are biased in different scenarios. The point is, while power is important, we must also understand the quality of our estimates.