Musings on missing data

MCAR

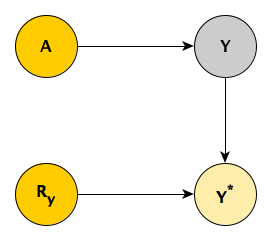
First, consider when the missingness is MCAR, as depicted above. From the DAG,    \(A \cup Y \perp \! \! \! \perp R_y\), since \(Y^*\) is a “collider”. It follows that \(P(A, Y) = P(A, Y \ | \ R_y)\), or more specifically \(P(A, Y) = P(A, Y \ | \ R_y=0)\). And when \(R_y = 0\), by definition \(Y = Y^*\). So we end up with \(P(A, Y) = P(A, Y^* \ | \ R_y = 0)\). Using observed data only, we can “recover” the underlying relationship between \(A\) and \(Y\).

A simulation my help to see this. First, we use the simstudy functions to define both the data generation and missing data processes:

def <- defData(varname = "a", formula = 0, variance = 1, dist = "normal")
def <- defData(def, "y", formula = "1*a", variance = 1, dist = "normal")

defM <- defMiss(varname = "y", formula = 0.2, logit.link = FALSE)

The complete data are generated first, followed by the missing data matrix, and ending with the observed data set.

set.seed(983987)

dcomp <- genData(1000, def)
dmiss <- genMiss(dcomp, defM, idvars = "id")
dobs <- genObs(dcomp, dmiss, "id")

head(dobs)

##    id      a     y
## 1:  1  0.171  0.84
## 2:  2 -0.882  0.37
## 3:  3  0.362    NA
## 4:  4  1.951  1.62
## 5:  5  0.069 -0.18
## 6:  6 -2.423 -1.29

In this replication, about 22% of the \(Y\) values are missing:

dmiss[, mean(y)]

## [1] 0.22

If \(P(A, Y) = P(A, Y^* \ | \ R_y = 0)\), then we would expect that the mean of \(Y\) in the complete data set will equal the mean of \(Y^*\) in the observed data set. And indeed, they appear quite close:

round(c(dcomp[, mean(y)], dobs[, mean(y, na.rm = TRUE)]), 2)

## [1] 0.03 0.02

Going beyond the mean, we can characterize the joint distribution of \(A\) and \(Y\) using a linear model (which we know is true, since that is how we generated the data). Since the outcome data are missing completely at random, we would expect that the relationship between \(A\) and \(Y^*\) to be very close to the true relationship represented by the complete (and not fully observed) data.

fit.comp <- lm(y ~ a, data = dcomp)
fit.obs <- lm(y ~ a, data = dobs)

broom::tidy(fit.comp)

## # A tibble: 2 x 5
##   term        estimate std.error statistic   p.value
##   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept) -0.00453    0.0314    -0.144 8.85e-  1
## 2 a            0.964      0.0313    30.9   2.62e-147

broom::tidy(fit.obs)

## # A tibble: 2 x 5
##   term        estimate std.error statistic   p.value
##   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept)  -0.0343    0.0353    -0.969 3.33e-  1
## 2 a             0.954     0.0348    27.4   4.49e-116

And if we plot those lines over the actual data, they should be quite close, if not overlapping. In the plot below, the red points represent the true values of the missing data. We can see that missingness is scattered randomly across values of \(A\) and \(Y\) - this is what MCAR data looks like. The solid line represents the fitted regression line based on the full data set (assuming no data are missing) and the dotted line represents the fitted regression line using complete cases only.

dplot <- cbind(dcomp, y.miss = dmiss$y)

ggplot(data = dplot, aes(x = a, y = y)) +
  geom_point(aes(color = factor(y.miss)), size = 1) +
  scale_color_manual(values = c("grey60", "#e67c7c")) +
  geom_abline(intercept = coef(fit.comp)[1], 
              slope = coef(fit.comp)[2]) +
  geom_abline(intercept = coef(fit.obs)[1], 
              slope = coef(fit.obs)[2], lty = 2) +
  theme(legend.position = "none",
        panel.grid = element_blank())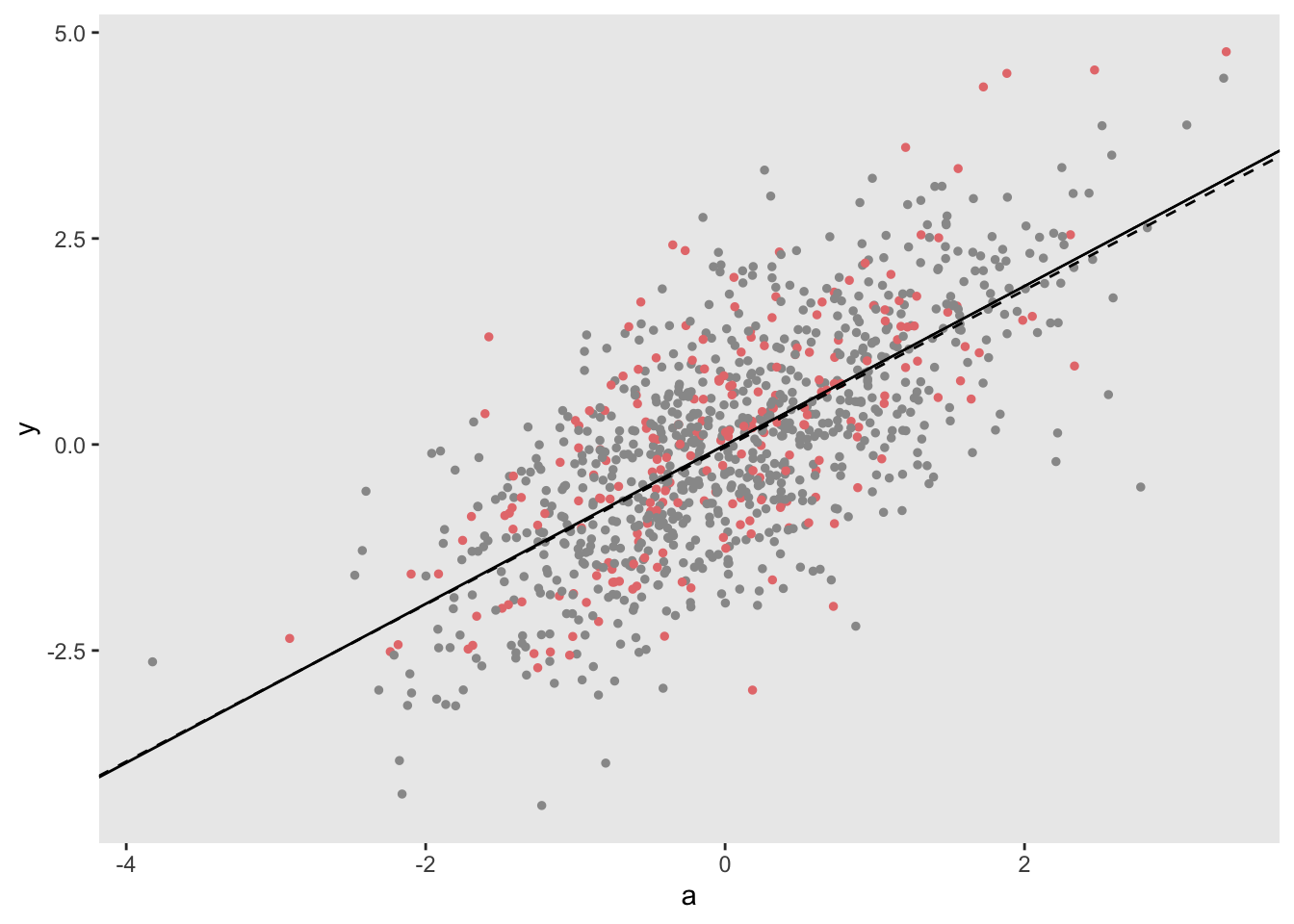

MAR

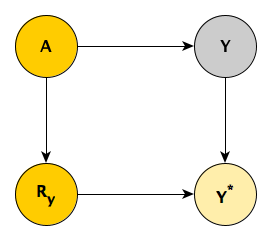
This DAG is showing a MAR pattern, where \(Y \perp \! \! \! \perp R_y \ | \ A\), again because \(Y^*\) is a collider. This means that \(P(Y | A) = P(Y | A, R_y)\). If we decompose \(P(A, Y) = P(Y | A)P(A)\), you can see how that independence is useful. Substituting \(P(Y | A, R_y)\) for \(P(Y | A)\) , \(P(A, Y) = P(Y | A, R_y)P(A)\). Going further, \(P(A, Y) = P(Y | A, R_y=0)P(A)\), which is equal to \(P(Y^* | A, R_y=0)P(A)\). Everything in this last decomposition is observable - \(P(A)\) from the full data set and \(P(Y^* | A, R_y=0)\) from the records with observed \(Y\)’s only.

This implies that, conceptually at least, we can estimate the conditional probability distribution of observed-only \(Y\)’s for each level of \(A\), and then pool the distributions across the fully observed distribution of \(A\). That is, under an assumption of data MAR, we can recover the joint distribution of the full data using observed data only.

To simulate, we keep the data generation process the same as under MCAR; the only thing that changes is the missingness generation process. \(P(R_y)\) now depends on \(A\):

defM <- defMiss(varname = "y", formula = "-2 + 1.5*a", logit.link = TRUE)

After generating the data as before, the proportion of missingness is unchanged (though the pattern of missingness certainly is):

dmiss[, mean(y)]

## [1] 0.22

We do not expect the marginal distribution of \(Y\) and \(Y^*\) to be the same (only the distributions conditional on \(A\) are close), so the means should be different:

round(c(dcomp[, mean(y)], dobs[, mean(y, na.rm = TRUE)]), 2)

## [1]  0.03 -0.22

However, since the conditional distribution of \((Y|A)\) is equivalent to \((Y^*|A, R_y = 0)\), we would expect estimates from a regression model of \(E[Y] = \beta_0 + \beta_1A)\) would yield estimates very close to \(E[Y^*] = \beta_0^{*} + \beta_1^{*}A\). That is, we would expect \(\beta_1^{*} \approx \beta_1\).

## # A tibble: 2 x 5
##   term        estimate std.error statistic   p.value
##   <chr>          <dbl>     <dbl>     <dbl>     <dbl>
## 1 (Intercept) -0.00453    0.0314    -0.144 8.85e-  1
## 2 a            0.964      0.0313    30.9   2.62e-147

## # A tibble: 2 x 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)  0.00756    0.0369     0.205 8.37e- 1
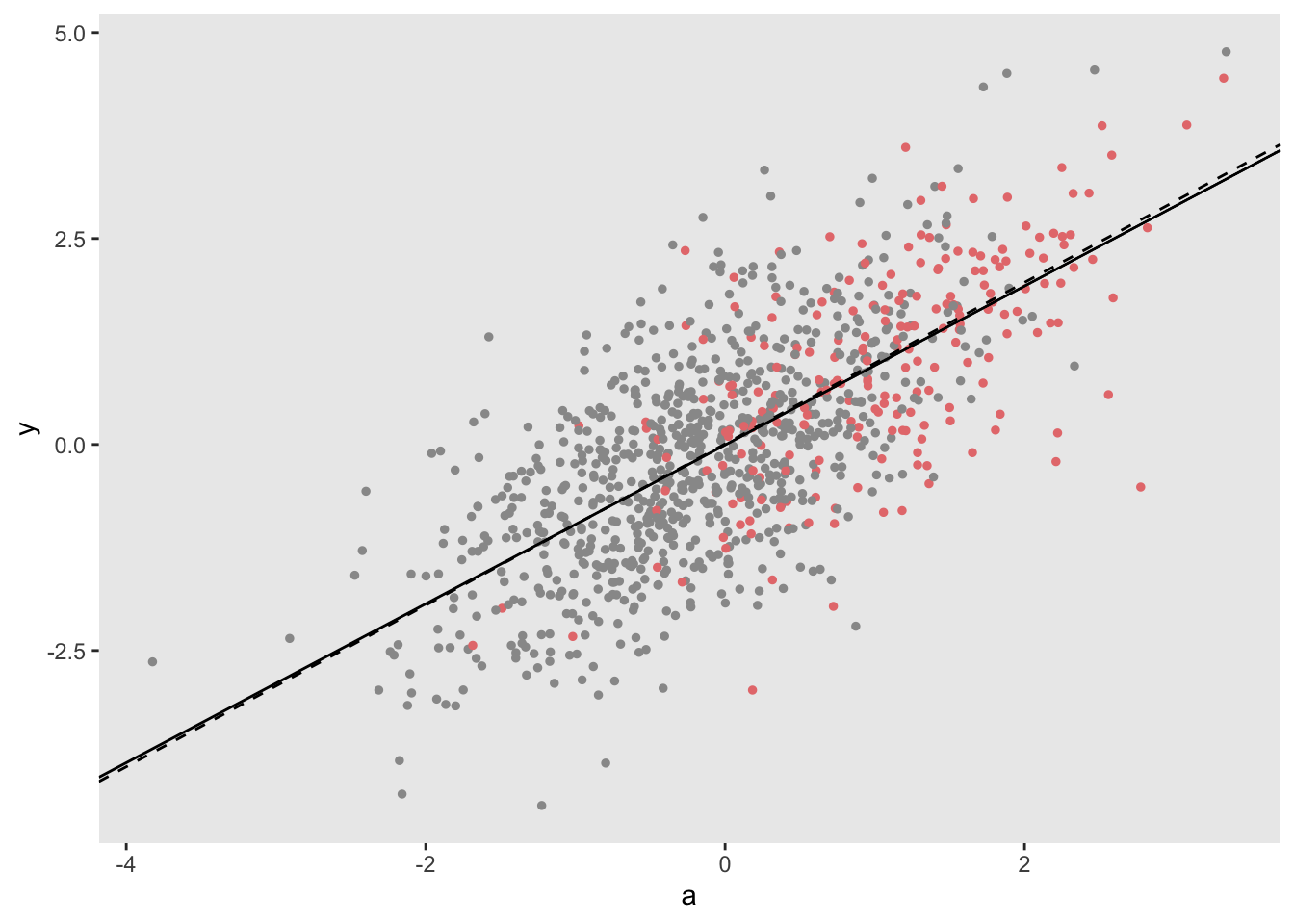
## 2 a            0.980      0.0410    23.9   3.57e-95

The overlapping lines in the plot confirm the close model estimates. In addition, you can see here that missingness is associated with higher values of \(A\).

MNAR

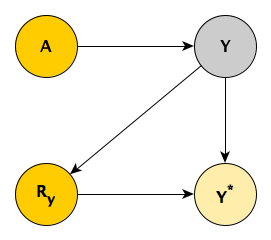
In MNAR, there is no way to separate \(Y\) from \(R_y\). Reading from the DAG, \(P(Y) \neq P(Y^* | R_y),\) and \(P(Y|A) \neq P(Y^* | A, R_y),\) There is no way to recover the joint probability of \(P(A,Y)\) with observed data. Mohan et al do show that under some circumstances, it is possible to use observed data to recover the true distribution under MNAR (particularly when there is missingness related to the exposure measurement \(A\)), but not in this particular case.

Daniel et al have a different approach to determine whether the causal relationship of \(A\) and \(Y\) is identifiable under the different mechanisms. They do not use a variable like \(Y^*\), but introduce external nodes \(U_a\) and \(U_y\) representing unmeasured variability related to both exposure and outcome (panel a of the diagram below).

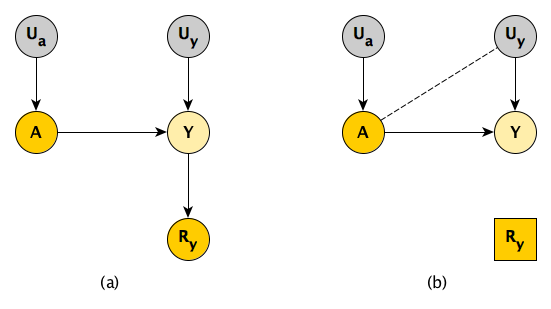
In the case of MNAR, when you use complete cases only, you are effectively controlling for \(R_y\) (panel b). Since \(Y\) is a collider (and \(U_y\) is an ancestor of \(Y\)), this has the effect of inducing an association between \(A\) and \(U_y\), the common causes of \(Y\). By doing this, we have introduced unmeasured confounding that cannot be corrected, because \(U_y\), by definition, always represents the portion of unmeasured variation of \(Y\).

In the simulation, I explicitly generate \(U_y\), so we can see if we observe this association:

def <- defData(varname = "a", formula = 0, variance = 1, dist = "normal")
def <- defData(def, "u.y", formula = 0, variance = 1, dist = "normal")
def <- defData(def, "y", formula = "1*a + u.y", dist = "nonrandom")

This time around, we generate missingness of \(Y\) as a function of \(Y\) itself:

defM <- defMiss(varname = "y", formula = "-3 + 2*y", logit.link = TRUE)

And this results in just over 20% missingness:

dmiss[, mean(y)]

## [1] 0.21

Indeed, \(A\) and \(U_y\) are virtually uncorrelated in the full data set, but are negatively correlated in the cases where \(Y\) is not missing, as theory would suggest:

round(c(dcomp[, cor(a, u.y)], dobs[!is.na(y), cor(a, u.y)]), 2)

## [1] -0.04 -0.23

The plot generated from these data shows diverging regression lines, the divergence a result of the induced unmeasured confounding.

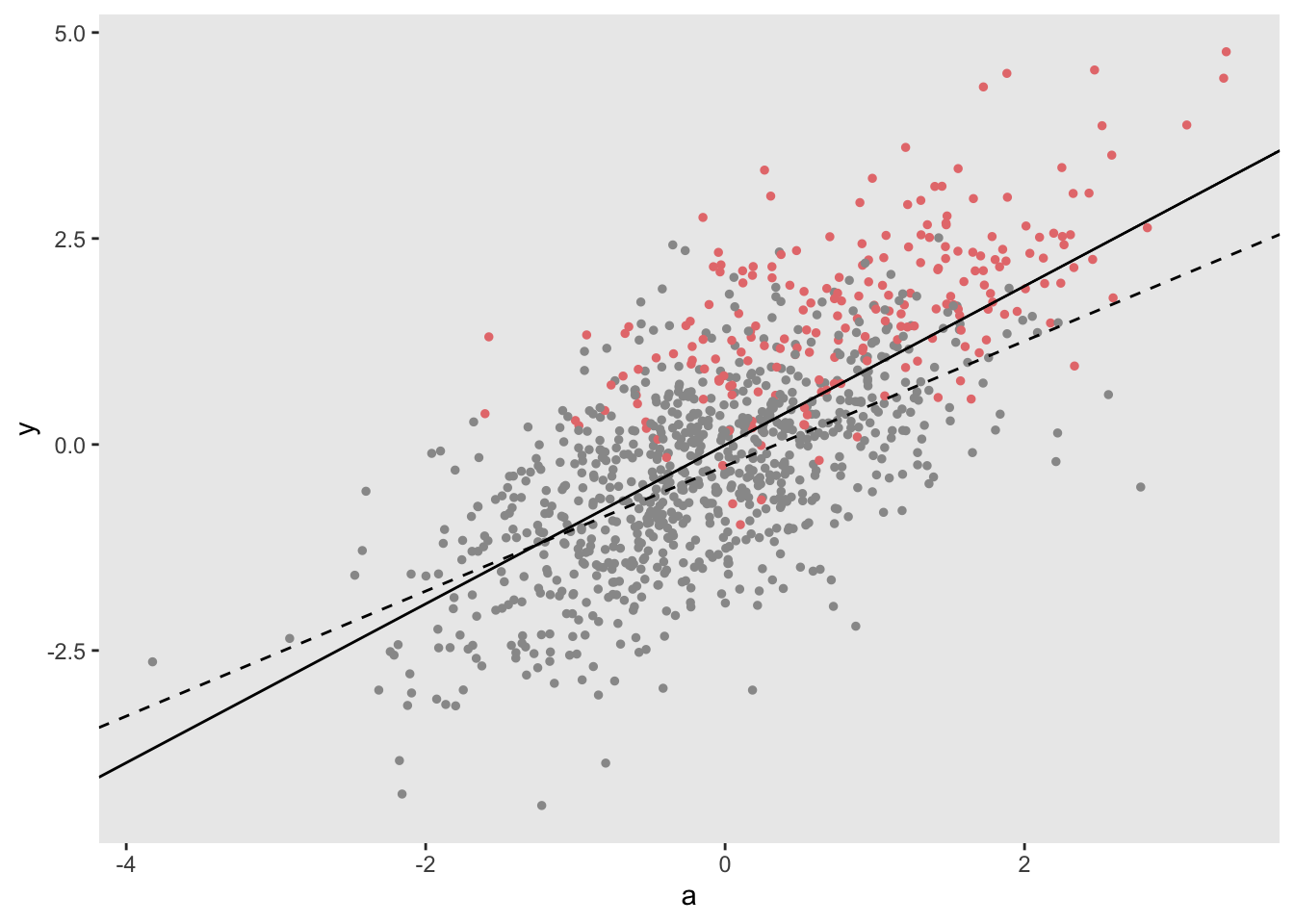
In this MNAR example, we see that the missingness is indeed associated with higher values of \(Y\), although the proportion of missingness remains at about 21%, consistent with the earlier simulations.