I am putting together a brief lecture introducing causal inference for graduate students studying biostatistics. As part of this lecture, I thought it would be helpful to spend a little time describing directed acyclic graphs (DAGs), since they are an extremely helpful tool for communicating assumptions about the causal relationships underlying a researcher’s data.
The strength of DAGs is that they help us think how these underlying relationships in the data might lead to biases in causal effect estimation, and suggest ways to estimate causal effects that eliminate these biases. (For a real introduction to DAGs, you could take a look at this paper by Greenland, Pearl, and Robins or better yet take a look at Part I of this book on causal inference by Hernán and Robins.)
As part of this lecture, I plan on including a (frustrating) example that illustrates a scenario where it may in fact be impossible to get an unbiased estimate of the causal effect of interest based on the data that has been collected. I thought I would share this little example here.
The scenario
In the graph below we are interested in the causal effect of \(A\) on an outcome \(Y\). We have also measured a covariate \(L\), thinking it might be related to some unmeasured confounder (in this case \(U_2\)). Furthermore, there is another unmeasured variable \(U_1\) unrelated to \(A\), but related to the measure \(L\) and outcome \(Y\). These relationships are captured in this DAG:
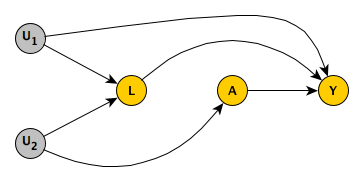
It may help to be a bit more concrete about what these variables might represent. Say we are conducting an epidemiological study focused on whether or not exercise between the age of 50 and 60 has an effect on hypertension after 60. (So, \(A\) is exercise and \(Y\) is a measure of hypertension.) We are concerned that there might be confounding by some latent (unmeasured) factor related to an individual’s conscientiousness about their health; those who are more conscientious may exercise more, but they will also do other things to improve their health. In this case, we are able to measure whether or not the individual has a healthy diet (\(L\)), and we hope that will address the issue of confounding. (Note we are making the assumption that conscientiousness is related to hypertension only through exercise or diet, probably not very realistic.)
But, it also turns out that an individual’s diet is also partly determined by where the individual lives; that is, characteristics of the area may play a role. Unfortunately, the location of the individual (or characteristics of the location) was not measured (\(U_1\)). These same characteristics also affect location-specific hypertension levels.
Inspecting the original DAG, we see that \(U_2\) is indeed confounding the relationship between \(A\) and \(Y\). There is a back-door path \(A \rightarrow U_2 \rightarrow L \rightarrow Y\) that needs to be blocked. We cannot just ignore this path. If we generate data and estimate the effect of \(A\) on \(Y\), we will see that the estimate is quite biased. First, we generate data based on the DAG, assuming \(L\), and \(A\) are binary, and \(Y\) is continuous (though this is by no means necessary):
d <- defData(varname = "U1", formula = 0.5,
dist = "binary")
d <- defData(d, varname = "U2", formula = 0.4,
dist = "binary")
d <- defData(d, varname = "L", formula = "-1.6 + 1 * U1 + 1 * U2",
dist = "binary", link = "logit")
d <- defData(d, varname = "A", formula = "-1.5 + 1.2 * U2",
dist = "binary", link="logit")
d <- defData(d, varname = "Y", formula = "0 + 1 * U1 + 1 * L + 0.5 * A",
variance = .5, dist = "normal")
set.seed(20190226)
dd <- genData(2500, d)
dd## id U1 U2 L A Y
## 1: 1 0 1 1 1 1.13
## 2: 2 0 0 1 0 1.31
## 3: 3 1 0 0 0 1.20
## 4: 4 0 1 1 0 1.04
## 5: 5 0 0 0 0 -0.67
## ---
## 2496: 2496 0 0 0 0 0.29
## 2497: 2497 0 0 0 0 -0.24
## 2498: 2498 1 0 1 0 1.32
## 2499: 2499 1 1 1 1 3.44
## 2500: 2500 0 0 0 0 -0.78And here is the unadjusted model. The effect of \(A\) is overestimated (the true effect is 0.5):
broom::tidy(lm(Y ~ A, data = dd))## # A tibble: 2 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 0.826 0.0243 34.0 2.54e-208
## 2 A 0.570 0.0473 12.0 1.53e- 32Adjusting for a potential confounder that is also a collider
While we are not able to measure \(U_2\), we have observed \(L\). We might think we are OK. But, alas, we are not. If we control for diet (\(L\)), we are controlling a “collider”, which will open up an association between \(U_1\) and \(U_2\). (I wrote about this before here.)
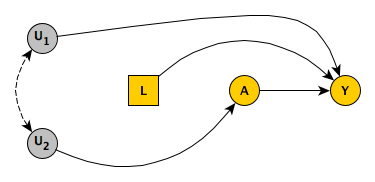
The idea is that if I have a healthy diet but I am not particularly conscientious about my health, I probably live in an area encourages or provides access to better food. Therefore, conditioning on diet induces a (negative, in this case) correlation between location type and health conscientiousness. So, by controlling \(L\) we’ve created a back-door path \(A \rightarrow U_2 \rightarrow U_1 \rightarrow Y\). Confounding remains, though it may be reduced considerably if the induced link between \(U_2\) and \(U_1\) is relatively weak.
broom::tidy(lm(Y ~ L+ A, data = dd))## # A tibble: 3 x 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 0.402 0.0231 17.4 6.58e- 64
## 2 L 1.26 0.0356 35.6 2.10e-224
## 3 A 0.464 0.0386 12.0 2.46e- 32More systematic exploration of bias and variance of estimates
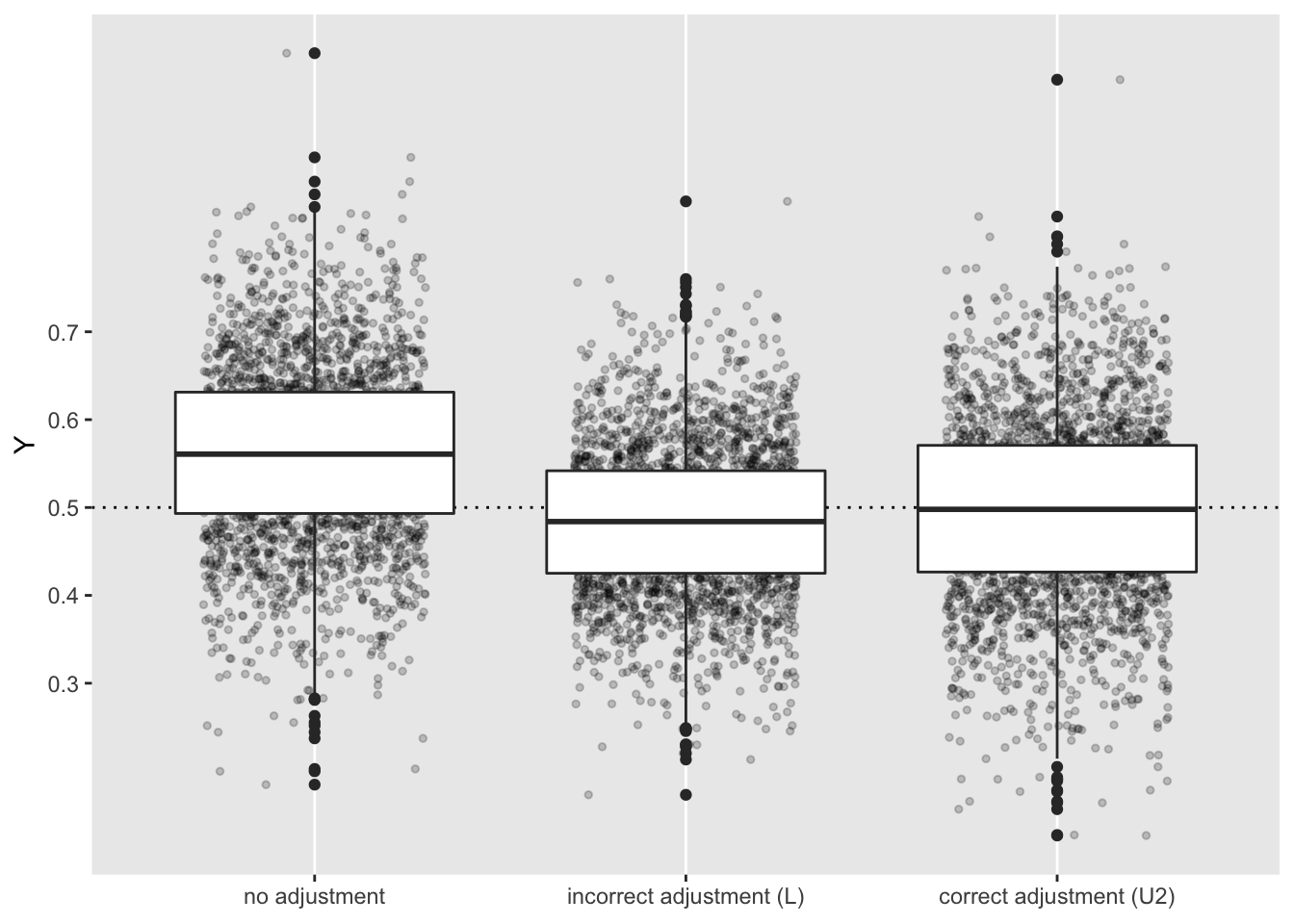
If we repeatedly generate samples (this time of size 500), we get a much better picture of the consequences of using different models to estimate the causal effect. The function below generates the data (using the same definitions as before), and then estimating three different models: (1) no adjustment, (2) incorrect adjustment for \(L\), the confounder/collider, and (3) the correct adjustment of the unmeasured confounder \(U_2\), which should be unbiased. The function returns the three estimates of the causal effect of \(A\):
repFunc <- function(n, def) {
dd <- genData(n, def)
c1 <- coef(lm(Y ~ A, data = dd))["A"]
c2 <- coef(lm(Y ~ L + A, data = dd))["A"]
c3 <- coef(lm(Y ~ U2 + A, data = dd))["A"]
return(data.table(c1, c2, c3))
}This following code generates 2500 replications of the “experiment” and stores the final results in data.table rdd:
RNGkind("L'Ecuyer-CMRG") # to set seed for parallel process
reps <- parallel::mclapply(1:2500,
function(x) repFunc(500, d),
mc.set.seed = TRUE)
rdd <- rbindlist(reps)
rdd[, rep := .I]
rdd## c1 c2 c3 rep
## 1: 0.46 0.45 0.40 1
## 2: 0.56 0.45 0.41 2
## 3: 0.59 0.46 0.50 3
## 4: 0.74 0.68 0.61 4
## 5: 0.45 0.43 0.41 5
## ---
## 2496: 0.42 0.42 0.37 2496
## 2497: 0.57 0.54 0.53 2497
## 2498: 0.56 0.49 0.51 2498
## 2499: 0.53 0.45 0.43 2499
## 2500: 0.73 0.63 0.69 2500rdd[, .(mean(c1 - 0.5), mean(c2 - 0.5), mean(c3-0.5))]## V1 V2 V3
## 1: 0.062 -0.015 -0.0016rdd[, .(var(c1), var(c2), var(c3))]## V1 V2 V3
## 1: 0.011 0.0074 0.012As expected, the first two models are biased, whereas the third is not. Under these parameter and distribution assumptions, the variance of the causal effect estimate is larger for the unbiased estimate than for the model that incorrectly adjusts for diet (\(L\)). So, we seem to have a bias/variance trade-off. In other cases, where we have binary outcome \(Y\) or continuous exposures, this trade-off may be more or less extreme.
Here, we end with a look at the estimates, with the dashed line indicated at the true causal effect of \(A\) on \(Y\):
