This is the context. In the convalescent plasma pooled individual patient level meta-analysis we are conducting as part of the COMPILE study, there is great interest in understanding the impact of antibody levels on outcomes. (I’ve described various aspects of the analysis in previous posts, most recently here). In other words, not all convalescent plasma is equal.
If we had a clear measure of antibodies, we could model the relationship of these levels with the outcome of interest, such as health status as captured by the WHO 11-point scale or mortality, and call it a day. Unfortunately, at the moment, there is no single measure across the RCTs included in the meta-analysis (though that may change). Until now, the RCTs have used a range of measurement “platforms” (or technologies), which may measure different components of the convalescent plasma using different scales. Given these inconsistencies, it is challenging to build a straightforward model that simply estimates the relationship between antibody levels and clinical outcomes.
The study team is coalescing around the idea of comparing the outcomes of patients who received low levels of antibodies with patients who received not low levels (as well as with patients who received no antibodies). One thought (well, really my thought) is to use a model that can jointly estimate the latent threshold and, given that threshold, estimate a treatment effect. Importantly, this model would need to accommodate multiple antibody measures and their respective thresholds.
To tackle this problem, I have turned to a class of models called change point or threshold models. My ultimate goal is to fit a Bayesian model that can estimate threshold and effect-size parameters for any number of RCTs using any number of antibody measures. At this point we are a few steps removed from that, so in this post I’ll start with a simple case of a single RCT and a single antibody measure, and use a maximum likelihood estimation method implemented in the R package chngpt to estimate parameters from a simulated data set. In a subsequent post, I’ll implement a Bayesian version of this simple model, and perhaps in a third post, I’ll get to the larger model that incorporates more complexity.
Visualizing simple scenarios
Change point models appear to be most commonly used in the context of time series data where the focus is on understanding if a trend or average has shifted at a certain point in a sequence of measurements over time. In the case of COMPILE, the target would be a threshold for a continuous antibody measure across multiple patients; we are interested in measuring the average outcome for patients on either side of the threshold.
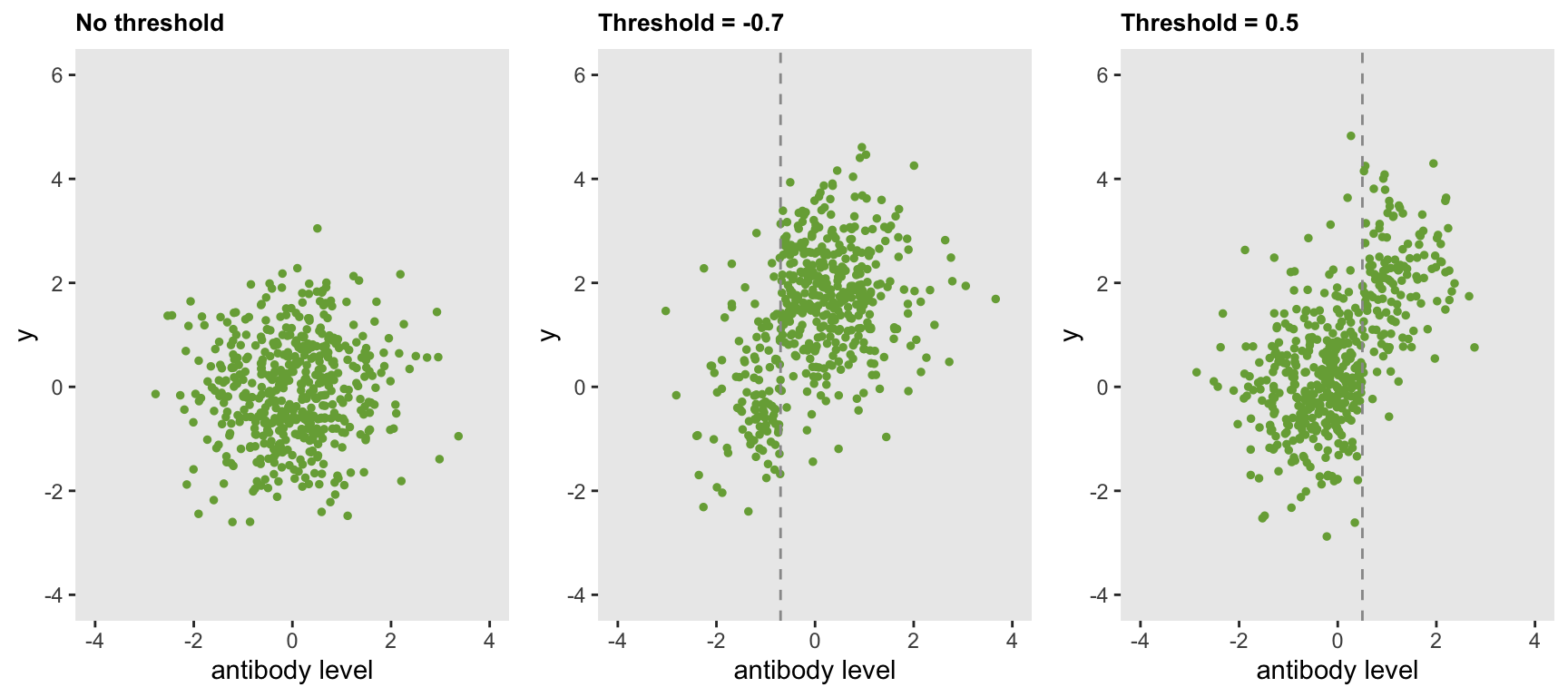
The following plots show three scenarios. On the left, there is no threshold; the distribution of continuous outcomes is the same across all values of the the antibody measure. In the middle, there is a threshold at ; patients with antibody levels below have a lower average outcome than patients with antibodies above . On the right, the threshold is shifted to .
The key here is that the outcome is solely a function of the latent categorical status - not the actual value of the antibody level. This may be a little simplistic, because we might expect the antibody level itself to be related to the outcome based on some sort of linear or non-linear relationship rather than the dichotomous relationship we are positing here. However, if we set our sights on detecting a difference in average clinical outcomes for patients categorized as having been exposed to low and not low antibody levels rather than on understanding the full nature of their relationship, this simplification may be reasonable.
Data generation
I think if you see the data generation process, the model and assumptions might make more sense. We start with an antibody level that, for simplicity’s sake, has a standard normal distribution. In this simulation, the latent group status (i.e. low vs. not low) is not determined completely by the threshold (though it certainly could); here, the probability that latent status is not low is about for patients with antibody levels that fall below , but is for patients that exceed threshold.
library(simstudy)
set.seed(87654)
d1 <- defData(varname = "antibody", formula = 0, variance = 1, dist = "normal")
d1 <- defData(d1, varname = "latent_status", formula = "-3 + 6 * (antibody > -0.7)",
dist = "binary", link = "logit")
d1 <- defData(d1, varname = "y", formula = "0 + 3 * latent_status",
variance = 1, dist = "normal")
dd <- genData(500, d1)
dd## id antibody latent_status y
## 1: 1 -1.7790 0 0.5184
## 2: 2 0.2423 1 3.2174
## 3: 3 -0.4412 1 1.8948
## 4: 4 -1.2505 0 0.9816
## 5: 5 -0.0552 1 2.9251
## ---
## 496: 496 -0.4634 1 2.7298
## 497: 497 0.6862 0 -0.0507
## 498: 498 -1.0899 0 0.9680
## 499: 499 2.3395 1 1.9540
## 500: 500 -0.4874 1 3.5238Simple model estimation
The chngptm function in the chngpt package provides an estimate of the threshold as well as the treatment effect of antibody lying above this latent threshold. The parameters in this simple case are recovered quite well. The fairly narrow confidence interval (2.2, 2.8) just misses the true value. The very narrow CI for the threshold is (-0.73, -0.69) just does include the true value.
library(chngpt)
fit <- chngptm(formula.1 = y ~ 1, formula.2 = ~ antibody,
data = dd, type="step", family="gaussian")
summary(fit)## Change point model threshold.type: step
##
## Coefficients:
## est Std. Error* (lower upper) p.value*
## (Intercept) 0.296 0.130 0.0547 0.563 2.26e-02
## antibody>chngpt 2.520 0.139 2.2416 2.787 1.99e-73
##
## Threshold:
## est Std. Error (lower upper)
## -0.70261 0.00924 -0.72712 -0.69092Alternative scenarios
When there is more ambiguity in the relationship between the antibody threshold and the classification into the two latent classes of low and not low, there is more uncertainty in both the effect and threshold estimates. Furthermore, the effect size estimate is attenuated, since the prediction of the latent class is less successful.
In the next simulation, the true threshold remains at , but the probability that a patient below the threshold actually does not have low levels of antibodies increases to about , while the probability of a patient above the threshold does not have low levels of antibodies decreases to . There is more uncertainty regarding the the threshold, as the CI is (-1.09, -0.62). And the estimated effect is is attenuated with more uncertainty. Given the added uncertainty in the data generation process, these estimates are what we would expect.
d1 <- updateDef(d1, changevar = "latent_status",
newformula = "-1.3 + 2.6 * (antibody > -0.7)")
dd <- genData(500, d1)
fit <- chngptm(formula.1 = y ~ 1, formula.2 = ~ antibody,
data = dd, type="step", family="gaussian")
summary(fit)## Change point model threshold.type: step
##
## Coefficients:
## est Std. Error* (lower upper) p.value*
## (Intercept) 0.881 0.159 0.50 1.12 3.05e-08
## antibody>chngpt 1.439 0.173 1.17 1.85 1.09e-16
##
## Threshold:
## est Std. Error (lower upper)
## -0.6298 0.0579 -0.8083 -0.5814The effect size has an impact on the estimation of a threshold. At the extreme case where there is no effect, the concept of a threshold is not meaningful; we would expect there to be great uncertainty with the estimate for the threshold. As the true effect size grows, we would expect the precision of the threshold estimate to increase as well (subject to the latent class membership probabilities just described). The subsequent plot shows the point estimates and CIs for thresholds at different effect sizes. The true threshold is and effect sizes range from 0 to 2:
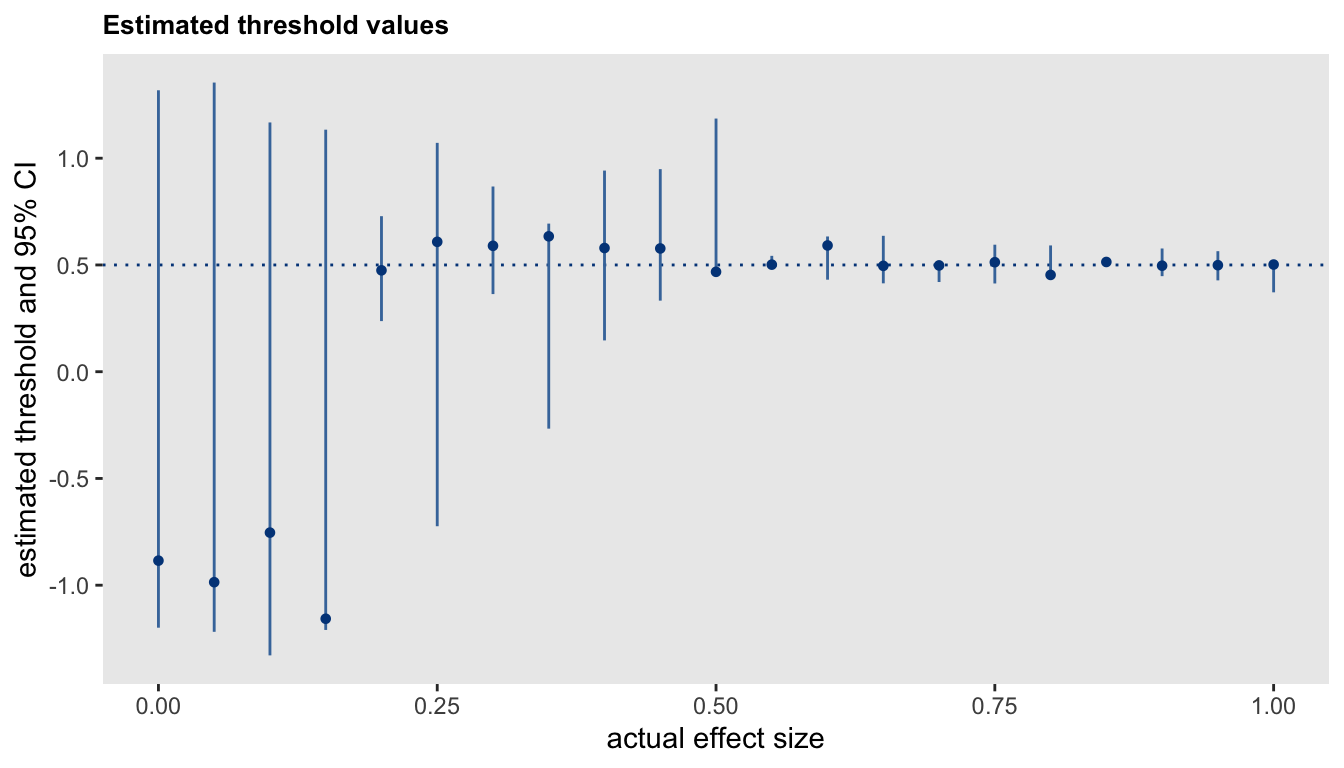
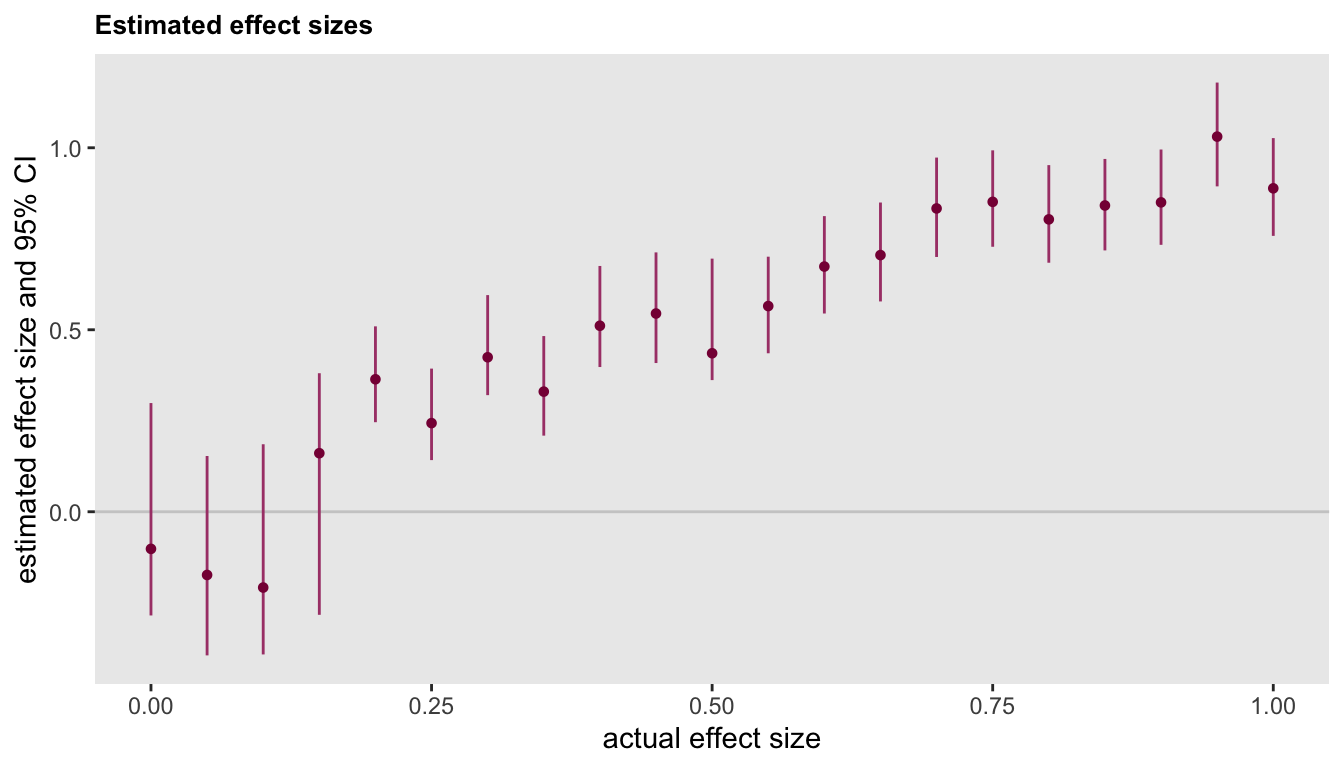
This last figure shows that the uncertainty around the effect size estimate is higher at lower levels of true effectiveness. This higher level of uncertainty in the estimated effect is driven by the higher level of uncertainty in the estimate of the threshold at lower effect sizes (as just pointed out above).
With a fundamentally different data generating process
What happens when the underlying data process is quite different from the one we have been imagining? Is the threshold model useful? I would say “maybe not” in the case of a single antibody measurement. I alluded to this a bit earlier in the post, justifying the idea by arguing it might make more sense with multiple types of antibody measurements. We will hopefully find that out if I get to that point. Here, I briefly investigate the estimates we get from a threshold model when the outcome is linearly related to the antibody measurement, and there is in fact no threshold, as in this data set:
d1 <- defData(varname = "antibody", formula = 0, variance = 1, dist = "normal")
d1 <- defData(d1, varname = "y", formula = "antibody", variance = 1, dist = "normal")
dd <- genData(500, d1)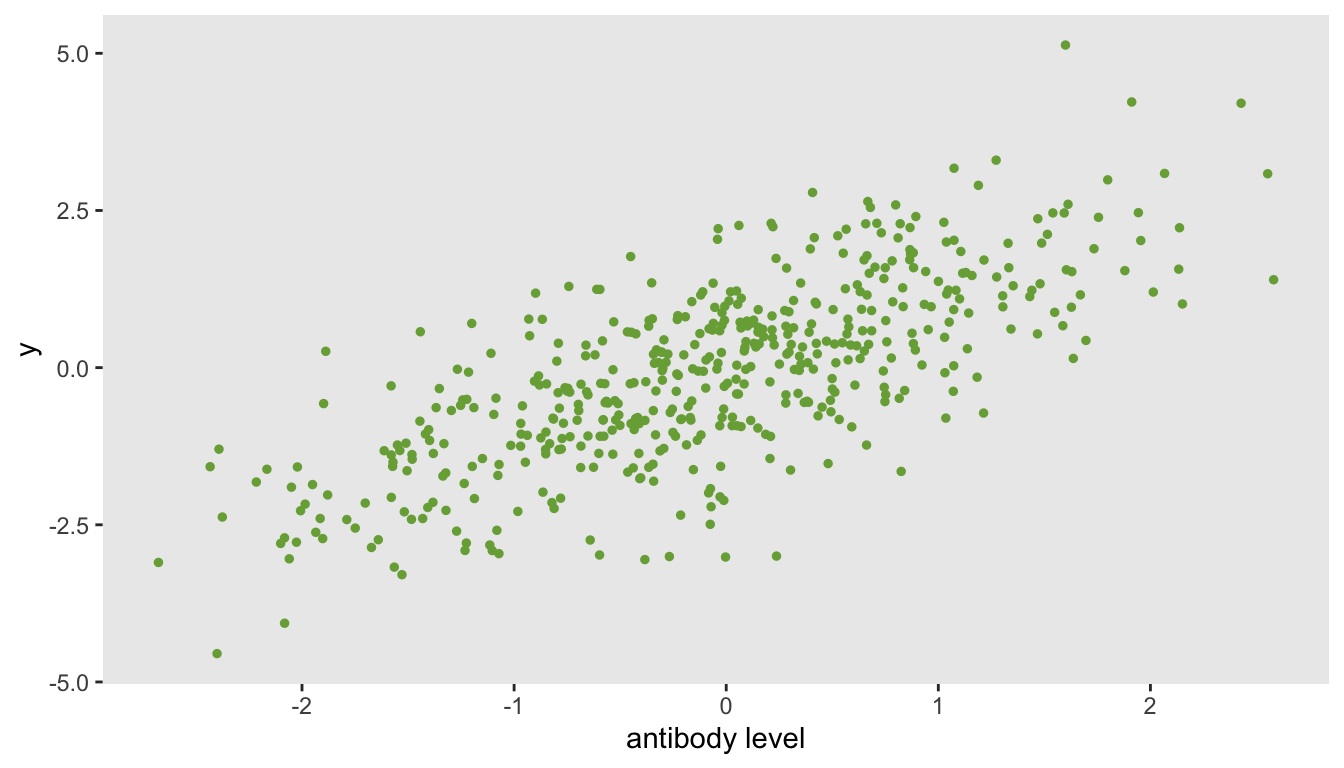
The estimated threshold is near the center of the antibody data (which in this case is close to ), with a fairly narrow confidence interval. The effect size is essentially a comparison of the means for patients with measurements below compared to patients above . If this were the actual data generation process, it might be preferable to model the relationship directly using simple linear regression without estimating a threshold.
fit <- chngptm(formula.1 = y ~ 1, formula.2 = ~ antibody,
data = dd, type="step", family="gaussian")
summary(fit)## Change point model threshold.type: step
##
## Coefficients:
## est Std. Error* (lower upper) p.value*
## (Intercept) -0.972 0.162 -1.24 -0.607 2.19e-09
## antibody>chngpt 1.739 0.109 1.58 2.006 1.15e-57
##
## Threshold:
## est Std. Error (lower upper)
## -0.0713 0.2296 -0.3832 0.5170