In recent discussions with a number of collaborators at the NIA IMPACT Collaboratory about setting the sample size for a proposed cluster randomized trial, the question of variable cluster sizes has come up a number of times. Given a fixed overall sample size, it is generally better (in terms of statistical power) if the sample is equally distributed across the different clusters; highly variable cluster sizes increase the standard errors of effect size estimates and reduce the ability to determine if an intervention or treatment is effective.
When I started to prepare a quick simulation to demonstrate this phenomenon, I quickly realized that there was no easy way using simstudy (my simulation package of choice) to generate the desired variable cluster sizes while holding the total sample size constant. I thought about it for a bit and came up with a simple solution that is now implemented and available for download (devtools::install_github("kgoldfeld/simstudy")). My plan here is to describe this solution, and then show the results of the simulation that inspired the need for (and uses) the new functionality.
Quick recap on how to generate cluster data with simstudy
There are two ways I would have typically simulated clustered data using a data generation process defined by a linear mixed-effects model. In both cases, we would define a variable \(n\) the represents the number of subjects per cluster.
In the first approach, we would assume perfectly balanced cluster sizes and fix \(n\) at a constant value. In the example, we will generate 10 clusters with 20 members each. In this case, I am generating the cluster-level random effect and treatment assignment. The individual-level outcome is a function of the treatment assignment and the cluster effect, as well as random individual-level variation. All of this is specified in the data generation definitions:
library(simstudy)
d0 <- defData(varname = "n", formula = 20, dist = "nonrandom")
d0 <- defData(d0, varname = "a", formula = 0, variance = 0.33)
d0 <- defData(d0, varname = "rx", formula = "1;1", dist = "trtAssign")
d1 <- defDataAdd(varname = "y", formula = "18 + 1.6 * rx + a",
variance = 16, dist = "normal")The data are generated in two steps. First, the cluster-level data are generated:
set.seed(2761)
dc <- genData(10, d0, "site")
dc## site n a rx
## 1: 1 20 -0.3548 1
## 2: 2 20 -1.1232 1
## 3: 3 20 -0.5963 0
## 4: 4 20 -0.0503 1
## 5: 5 20 0.0894 0
## 6: 6 20 0.5294 1
## 7: 7 20 1.2302 0
## 8: 8 20 0.9663 1
## 9: 9 20 0.0993 0
## 10: 10 20 0.6508 0And then the individual level data are generated, \(n = 20\) subjects for each site:
dd <- genCluster(dc, "site", "n", "id")
dd <- addColumns(d1, dd)
dd## site n a rx id y
## 1: 1 20 -0.355 1 1 17.7
## 2: 1 20 -0.355 1 2 16.2
## 3: 1 20 -0.355 1 3 19.2
## 4: 1 20 -0.355 1 4 20.6
## 5: 1 20 -0.355 1 5 14.7
## ---
## 196: 10 20 0.651 0 196 25.3
## 197: 10 20 0.651 0 197 22.1
## 198: 10 20 0.651 0 198 13.2
## 199: 10 20 0.651 0 199 15.6
## 200: 10 20 0.651 0 200 13.8If we want variable cluster sizes, we could slightly modify the data definitions so that \(n\) is no longer constant. (From here on out, I am just generating \(n\) and the cluster-level data without the random effects and treatment assignment, but I could have just as easily included the full data.) Here, I am using the Poisson distribution, but I could use the negative binomial distribution if I wanted more variation across clusters:
d0 <- defData(varname = "n", formula = 20, dist = "poisson")
genData(10, d0, "site")## site n
## 1: 1 13
## 2: 2 18
## 3: 3 21
## 4: 4 26
## 5: 5 25
## 6: 6 27
## 7: 7 23
## 8: 8 30
## 9: 9 23
## 10: 10 20This is great, but the total sample size is no longer fixed at 200 (here we have randomly generated 226 individuals). The total will vary from sample to sample. So, if we want to have both across-cluster variability and constant total sample size, we need a new approach.
New approach using simstudy
There is a new simstudy distribution called “clusterSize”, which requires two parameters: the (fixed) total sample size (input into the formula field) and a (non-negative) dispersion measure that represents the variability across clusters (input into the variance field). (The idea behind the data generation is described in the addendum.) If the dispersion is set to \(0\), then we will have constant cluster sizes:
d0 <- defData(varname = "n", formula = 200, variance = 0, dist = "clusterSize")
genData(10, d0, "site")## site n
## 1: 1 20
## 2: 2 20
## 3: 3 20
## 4: 4 20
## 5: 5 20
## 6: 6 20
## 7: 7 20
## 8: 8 20
## 9: 9 20
## 10: 10 20When we increase the dispersion, we start to introduce cluster-size variability but keep the overall sample size at 200:
d0 <- defData(varname = "n", formula = 200, variance = 0.2, dist = "clusterSize")
genData(10, d0, "site")## site n
## 1: 1 20
## 2: 2 28
## 3: 3 25
## 4: 4 24
## 5: 5 28
## 6: 6 22
## 7: 7 7
## 8: 8 13
## 9: 9 22
## 10: 10 11And we can have extreme variability with a very high dispersion value:
d0 <- defData(varname = "n", formula = 200, variance = 5, dist = "clusterSize")
genData(10, d0, "site")## site n
## 1: 1 10
## 2: 2 2
## 3: 3 17
## 4: 4 2
## 5: 5 49
## 6: 6 110
## 7: 7 1
## 8: 8 4
## 9: 9 1
## 10: 10 4Application: cluster-size variability and statistical power
I conducted a simulation experiment to assess the impact of the dispersion parameter on the estimated power for a cluster randomized trial with cluster-level effects. In the simulation (code is available here), I assumed 20 clusters (10 randomized to the experimental arm, 10 to the control arm) and a total of 500 participants (so on average 25 per arm).
The specific model I used to generate the data was
\[y_{ij} = 20 + 1.6 * A_{i} + a_{i} + e_{ij},\]
where \(y_{ij}\) is the continuous outcome for subject \(j\) in cluster \(i\). \(A_i\) is the treatment indicator for cluster \(i\), \(A_i = 1\) if cluster \(i\) has been randomized to the experimental arm, \(A_i = 0\) otherwise. \(a_i\) is the cluster-specific random effect, is normally distributed: \(a_i \sim N(\mu = 0, \sigma_a^2)\). \(e_{ij}\) is the (unmeasured) individual \(j\) effect, and is also normally distributed: \(e_{ij} \sim N(\mu =0, \sigma_e^2 = 16)\).
Statistical power is directly influenced by overall variability of the outcome, which in this case includes the cluster and individual level variation. Specifically, power is a function of the intra-class (or intra-cluster) correlation (ICC), which can be calculated using \[ICC = \frac{\sigma_a^2}{\sigma_a^2 + \sigma_e^2}.\] In the simulations, ICCs ranged from \(0.1\) to \(0.4\). Since \(\sigma_e^2\) was fixed, the variance \(\sigma^2_a\) was determined by the ICC.
The focus of these simulations is to provide a figure that illustrates the impact of cluster-size variability (with constant total sample size) on power. I used different dispersion assumptions, ranging from 0 to 0.5, to generate different data sets. For each of the 44 ICC/dispersion parameter combinations, I generated 50,000 data sets (yes, I used a high performance computing core) and estimated a linear mixed effect model for each. The power was calculated for each combination by looking at the proportion of the p-values less than 0.05. The figure below shows the results; it appears that both higher ICCs and cluster size variability lead to reduced power:
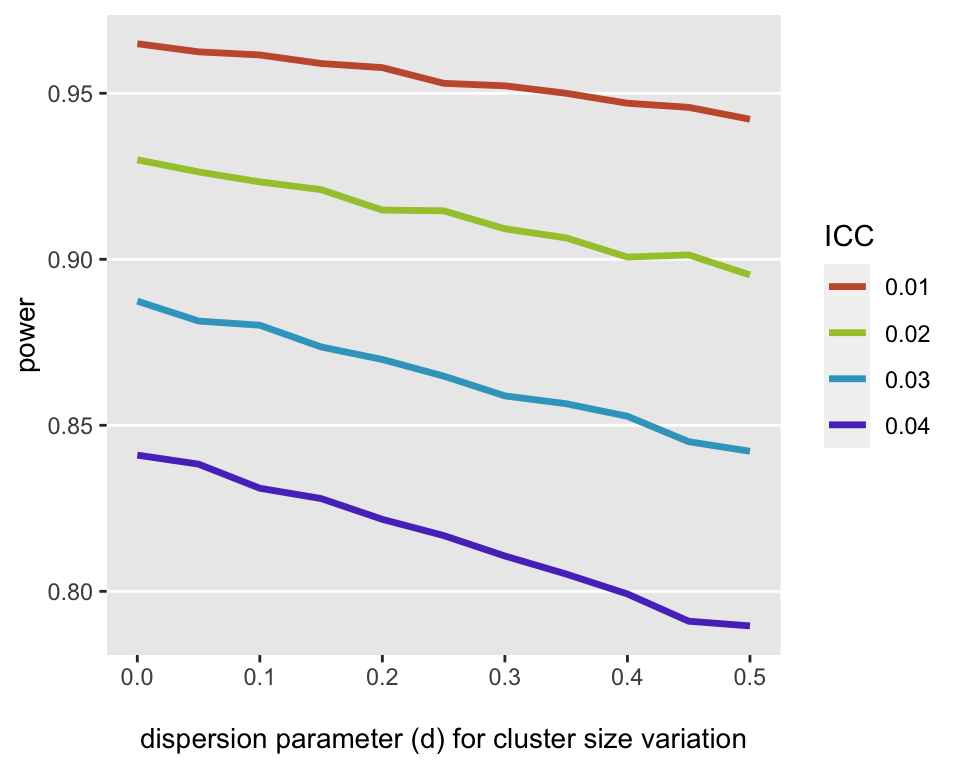
Given a particular ICC level, it seems pretty clear that cluster-size variability does matter when thinking about power. However, the impact may not be as substantial as the general variability in the outcome across the clusters. Unfortunately, I know of no analytic software that will provide insight into this. But if you are using simulation to conduct the sample size calculation, it is now extremely easy to incorporate cluster size variability into the simulations (particularly if you are using simstudy).
Support:
This work was supported in part by the National Institute on Aging (NIA) of the National Institutes of Health under Award Number U54AG063546, which funds the NIA IMbedded Pragmatic Alzheimer’s Disease and AD-Related Dementias Clinical Trials Collaboratory (NIA IMPACT Collaboratory). The author, a member of the Design and Statistics Core, was the sole writer of this blog post and has no conflicts. The content is solely the responsibility of the author and does not necessarily represent the official views of the National Institutes of Health.
Addendum - a simple trick to generate variation
Generating the variable cluster sizes under a fixed total is actually quite simple if you take advantage of the Dirichlet distribution. The Dirichlet distribution is essentially a multivariate generalization of the beta distribution. In the Dirichlet distribution, the multivariate values range from 0 to 1, and they sum to 1. Given the range of the data, it is very natural to use values generated from this distribution as probabilities or proportions, which is what the simstudy clusterSize distribution does. This is perhaps easiest to see in a simple example.
Values from the Dirichlet distribution can be generated using the rdirichlet function in the the dirmult package. The key parameter, called the concentration parameter, is a vector of length k, where k is the number of values (e.g. clusters) we are interested in generating. In the first example, I am generating 10 values using a concentration parameter of 32. (In the simstudy implementation of the clusterSize distribution, the dispersion parameter \(d\) is 1/concentration.)
Generating 20 values, we can see that all values are between 0 and 1, and sum to 1:
x <- dirmult::rdirichlet(1, alpha = rep(32, 20) )[1,]
x## [1] 0.0442 0.0465 0.0374 0.0506 0.0516 0.0516 0.0623 0.0429 0.0601 0.0404
## [11] 0.0490 0.0517 0.0589 0.0566 0.0320 0.0568 0.0458 0.0610 0.0542 0.0462sum(x)## [1] 1From here, it is easy generate values between 0 and 400 if we have a total sample size of 400.
s1 <- floor(x*400)
s1## [1] 17 18 14 20 20 20 24 17 24 16 19 20 23 22 12 22 18 24 21 18sum(s1)## [1] 389Due to rounding, the sum does not equal to 400. In the simstudy function this rounding error is accounted for by allocating an additional unit to randomly selected clusters.
If we use a lower concentration parameter (in this case 4), there should be more variability, and indeed there appears to be:
x <- dirmult::rdirichlet(1, alpha = rep(4, 20) )[1,]
s2 <- floor(x * 400)
s2## [1] 17 27 7 11 18 24 13 26 5 25 23 28 19 26 14 11 43 22 24 9It appears that the second sample is more variable than the first, and we can confirm this with the standard deviation:
c(sd1 = sd(s1), sd2 = sd(s2))## sd1 sd2
## 3.30 9.05