In the previous post, I described an incipient effort that I am undertaking with two colleagues, Monica Taljaard and Fan Li, to better understand the implications for collecting baseline measurements on sample size requirements for stepped wedge cluster randomized trials. (The three of us are on the Design and Statistics Core of the NIA IMPACT Collaboratory.) In that post, I conducted a series of simulations that illustrated the design effects in parallel cluster randomized trials derived analytically in a paper by Teerenstra et al. In this post, I am extending those simulations to stepped wedge trials; the hope is that the design effects can be formally derived some point soon.
Stepped wedge designs
At the end of the previous post, I provided links to a few earlier entries where I described stepped wedge designs in some detail. The first post I suggested provides an introductory overview.
In the stepped-wedge design, all clusters in a trial will receive the intervention at some point, but the start of the intervention at different sites will be staggered. The amount of time in each state (control or intervention) will differ for each cluster (or group of clusters if there are waves of more than one cluster starting up at the same time). In this design, time is divided into discrete data collection/phase-in periods.
In the figure below there are four waves of clusters (the rows), with sets of five clusters (the columns) in each wave. All waves are in the control condition in the first observation period, Wave 1 starts the intervention in period 2, Wave 2 starts in period 3, Wave 3 in period 4, and the last wave starts in period 5. Data from individuals in each cluster are collected for all periods, regardless of intervention status. The points in the figure represent individual (follow-up) responses within each cluster and time period.
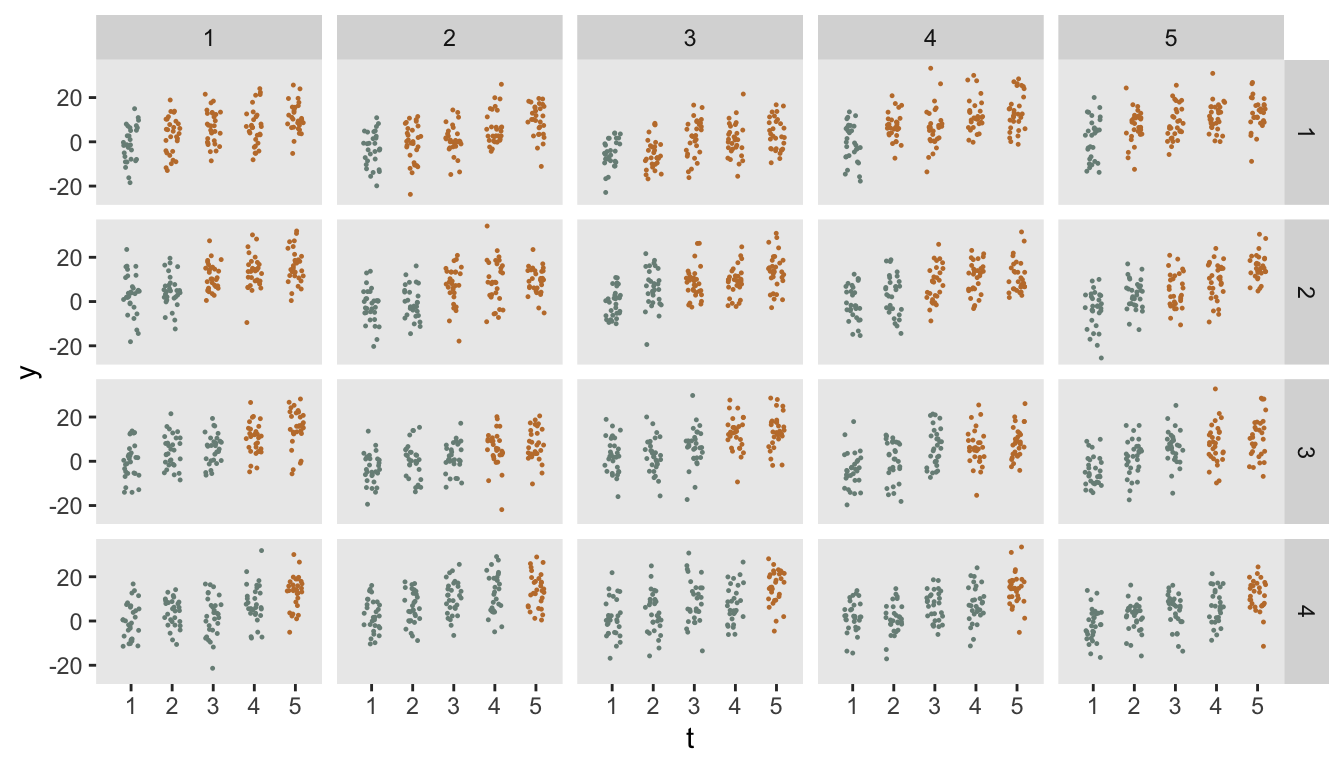
Data generation process
In order to accommodate a range of scenarios, I’ve written a general function base_sw that will be used in the data generating process (see addendum). This function allows for time period effects (specified as a time trend) as well as all the possible cluster and individual random effects. Importantly, this function will generate two outcome measures for each subject within a specific cluster and time period.
This is the general data generation process that I’ve used here:
\[ Y_{ijkt} = \tau (t-1) + \gamma k Z_{jt} + c_j + cp_{jt} + s_{ijt} + sp_{ijkt}, \]
where \(Y_{ijkt}\) is the outcome for subject \(i\) in cluster \(j\) measured in period \(t,\) \(t \in \{1,\dots, T\};\) \(k \in \{0, 1\}, \ k=0\) if the measurement is taken at baseline and \(k=1\) if the measurement is the follow-up. \(Z_{jt}\) is a treatment indicator for cluster \(j\) during period \(t\).
The parameter \(\tau\) is the general time trend. (The linear time trend is not a requirement - it is just what I am using here to easily generate time period effects.) \(\gamma\) is the treatment effect, which can only impact follow-up measurements. \(c_j\) and \(cp_{jt}\) are the cluster and cluster-period specific random effects with distributions \(N(0, \sigma_c^2)\) and \(N(0, \sigma_{cp}^2)\), respectively. \(s_{ijt}\) is the subject-level effect (and is specific to period \(t\) since the subject is only observed in that period), \(s_{ijt} \sim N(0, \sigma_{s}^2)\). \(sp_{ijkt}\) is the measurement noise, \(sp_{ijkt} \sim N(0, \sigma_{sp}^2).\)
The code itself is a little involved, because there are two longitudinal processes that need to be combined - clusters are repeated over time and subjects are repeated over time within each cluster period. In addition, there are two possible layers of cluster and subject random effects.
Below are three plots of data generated from three possible scenarios, using ten sites divided into two waves. The first scenario includes cluster and subject specific effects, but no fixed or random period effects. The second adds fixed period effects, and the third adds both fixed and random period effects:
dd_1 <- base_sw(
effect = 1,
trend = 0,
nsites = 10,
nwaves = 2,
nperiods = 5,
n = 30,
s_c = 6,
s_cp = 0,
s_s = 44,
s_sp = 20
)
dd_2 <- base_sw(1, 3, 10, 2, 5, 30, 6, 0, 44, 20)
dd_3 <- base_sw(1, 3, 10, 2, 5, 30, 4, 2, 44, 20) 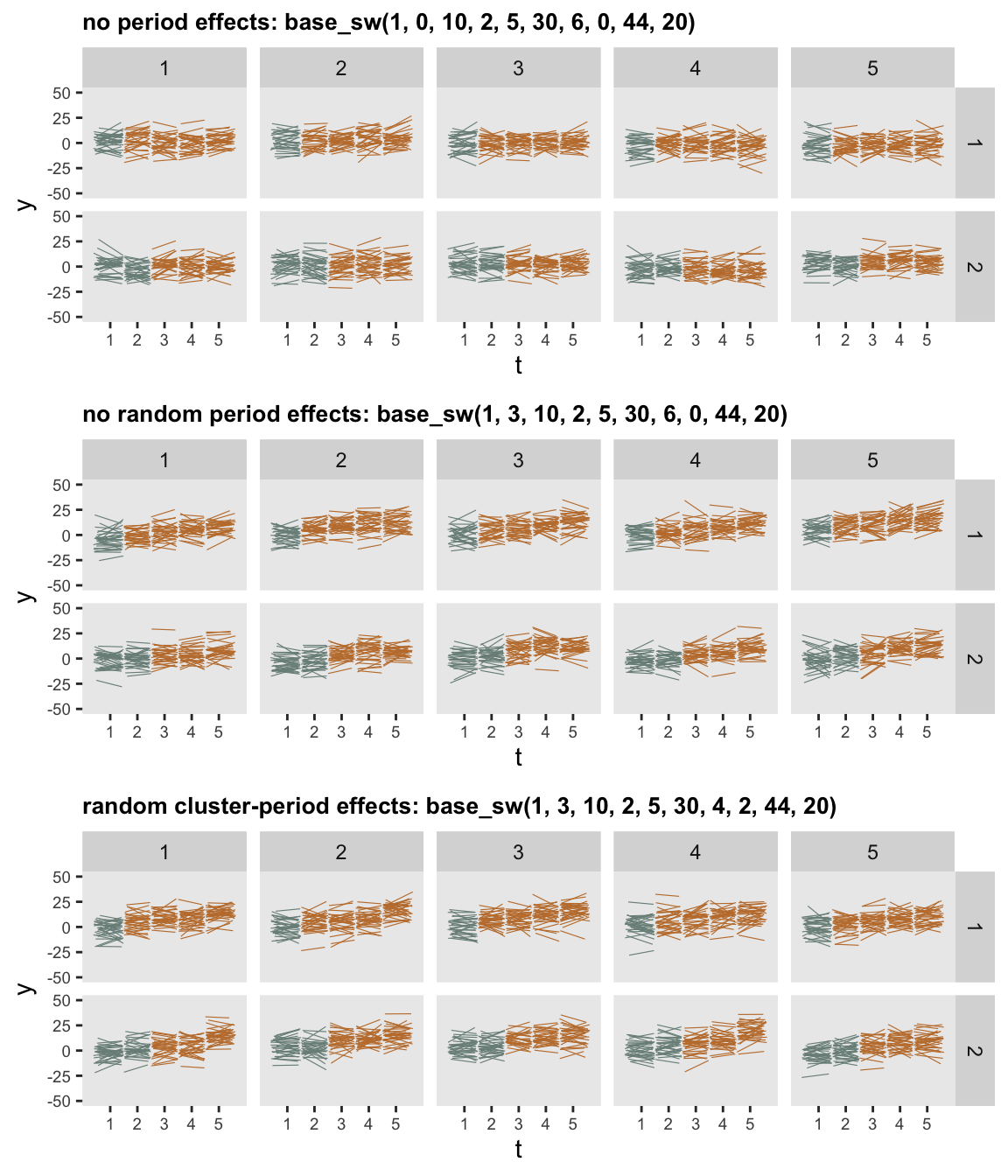
Models for estimating treatment effects
Of course, given a data set, there are many ways we can choose to analyze it. Which model we pick depends in large part on the structure of the data and the assumptions we are willing to make about the data generation process. Here, we describe five models, all of which are linear mixed effects models. Ideally, we will choose the one that provides the most information given the data on hand, and we hope these explorations might help clarify which of these is our best bet.
To start, we are focusing on a situation where there is no cluster-period effect (Scenario 2 from above), so that \(cp_{jt} = 0\) for all \(j\) and \(t\). The true effect size \(\gamma = 1\) and the time trend \(\tau = 3\). There will be 20 clusters divided into 4 waves of 5 clusters, with each wave starting in period \(t=1\), and the intervention is rolled out in periods 2 through 5, just as in the figure at the top. There will be 30 subjects for each cluster, each period. \(\sigma_c^2 = 6\), \(\sigma_{cp}^2 = 0\), \(\sigma_s^2 = 44\), and \(\sigma_{sp}^2 = 20.\) (See the second part of the addendum for examples from Scenarios 1 and 3.)
Here is a data set generated under these assumptions:
dd <- base_sw(1, 3, 20, 4, 5, 30, 6, 0, 44, 20)
dd[, t := factor(s_per, labels = c(1:5))]
dd## s_time site s_per id k c c.p s p_time startTrt Z y t
## 1: 1 1 0 1 0 2.4 0 -0.43 1 1 0 3.4 1
## 2: 1 1 0 1 1 2.4 0 -0.43 2 1 0 -7.6 1
## 3: 1 1 0 2 0 2.4 0 12.76 3 1 0 10.4 1
## 4: 1 1 0 2 1 2.4 0 12.76 4 1 0 9.4 1
## 5: 1 1 0 3 0 2.4 0 0.89 5 1 0 2.5 1
## ---
## 5996: 100 20 4 2998 1 -3.9 0 0.72 5996 4 1 12.5 5
## 5997: 100 20 4 2999 0 -3.9 0 3.29 5997 4 1 9.6 5
## 5998: 100 20 4 2999 1 -3.9 0 3.29 5998 4 1 16.0 5
## 5999: 100 20 4 3000 0 -3.9 0 0.86 5999 4 1 2.7 5
## 6000: 100 20 4 3000 1 -3.9 0 0.86 6000 4 1 8.8 5And here is a subset of the data that we will actually be able to observe in the real world, which will be used to estimate the models:
dd[, .(id, site, t, k, Z, y)]## id site t k Z y
## 1: 1 1 1 0 0 3.4
## 2: 1 1 1 1 0 -7.6
## 3: 2 1 1 0 0 10.4
## 4: 2 1 1 1 0 9.4
## 5: 3 1 1 0 0 2.5
## ---
## 5996: 2998 20 5 1 1 12.5
## 5997: 2999 20 5 0 1 9.6
## 5998: 2999 20 5 1 1 16.0
## 5999: 3000 20 5 0 1 2.7
## 6000: 3000 20 5 1 1 8.8Here is a description of each of the five models, along with code to estimate the models:
Model 1: Hussey & Hughes model with no baseline measurement
If we do not have access to the baseline data (or for some reason, choose to ignore it in the modeling), we could fit the stepped wedge model described by Hussey & Hughes:
\[ Y_{ijt} = \alpha_t + \gamma Z_{jt} + c_j + s_{ijt}, \]
where \(Y_{ijt}\) is the outcome for subject \(i\) in cluster \(j\) measured in period \(t\). \(Z_{jt}\) is a treatment indicator for cluster \(j\) during period \(t\). The \(\alpha_t\text{'s}\) are the period-specific fixed effects and \(\gamma\) is the treatment effect. \(c_j\) is the cluster specific random effects with distribution \(N(0, \sigma_c^2)\). \(s_{ijt}\) is the subject-level effect or noise, \(s_{ijt} \sim N(0, \sigma_{s}^2).\) Since there is only a single measurement for each subject, there is only a single subject-level effect. And because we have assumed no cluster-period random effects, \(cp_{jt}\) is not included in the model (and will also be the case for the other models described below).
This model can be estimated using the lmer function in package lme4. Note that we are using only the follow-up data in the model estimation:
d_std <- dd[k == 1]
fit_1 <- lmer( y ~ t + Z - 1 + (1|site), data = d_std)tbl_regression(fit_1, tidy_fun = broom.mixed::tidy) %>%
modify_footnote(ci ~ NA, abbreviation = TRUE)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| t | |||
| 1 | -0.73 | -1.9, 0.43 | 0.2 |
| 2 | 2.9 | 1.7, 4.1 | <0.001 |
| 3 | 5.0 | 3.8, 6.3 | <0.001 |
| 4 | 8.3 | 7.0, 9.7 | <0.001 |
| 5 | 11 | 9.7, 13 | <0.001 |
| Z | 1.0 | -0.03, 2.0 | 0.057 |
| site.sd__(Intercept) | 2.1 | ||
| Residual.sd__Observation | 7.9 |
The treatment and period effects are recovered quite well, as are the variance estimates of the random effects.
Model 2: Hussey & Hughes extended to baseline measurement
If we have access to both baseline and follow-up outcome measurements for each subject, we have a number of modeling options, four of which are described here. First, we can extend the Hussey & Hughes model to estimate the treatment effect. The baseline and follow-up measurements are assumed to be collected in the same period \(t\). The baseline measurement is collected prior to randomization (so will by definition be under the control condition). The follow-up measurement will be under the control or treatment condition, depending on the cluster and time period.
\[ Y_{ijkt} = \alpha_t + \gamma k Z_{jt} + c_j + s_{ijt} + sp_{ijkt}, \]
where \(Y_{ijkt}\) is outcome \(k\) for subject \(i\) in cluster \(j\) measured in period \(t\). \(k = 0\) when the measurement is from baseline and \(k=1\) when it is the follow-up. \(Z_{jt}\) is a treatment indicator for cluster \(j\) during period \(t\). The parameters \(\alpha_t\) and \(\gamma\) are the same as above. The random effect \(c_j\) is also unchanged from the previous model. The subject-level effects of this model are different, reflecting the fact that there are now two measurements per subject: \(s_{ijt}\) is the overall subject-level effect for subject \(i\) in cluster \(j\) during period \(t\), \(s_{ijt} \sim N(0,\sigma_s^2)\) and \(sp_{ijkt}\) is the measurement noise (which assumes that any two measurements from the same individual will vary), \(sp_{ijkt} \sim N(0,\sigma_{sp}^2)\).
Once again, the model estimates recover the true values pretty well:
fit_2 <- lmer(y ~ t + k:Z - 1 + (1|id:site) + (1|site), data = dd)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| t | |||
| 1 | -0.82 | -2.0, 0.33 | 0.2 |
| 2 | 2.8 | 1.6, 3.9 | <0.001 |
| 3 | 5.1 | 4.0, 6.3 | <0.001 |
| 4 | 8.2 | 7.0, 9.3 | <0.001 |
| 5 | 11 | 9.9, 12 | <0.001 |
| k * Z | 1.1 | 0.74, 1.4 | <0.001 |
| id:site.sd__(Intercept) | 6.5 | ||
| site.sd__(Intercept) | 2.1 | ||
| Residual.sd__Observation | 4.5 |
Model 3: Teerenstra et al difference in change model
In the previous post, I described a “difference in change” model proposed in a paper by Teerenstra et al for parallel designs. This can be extended to the context of a stepped wedge design:
\[ Y_{ijkt} = \alpha_t + \gamma_0 k + \gamma_1 Z_{jt} + \gamma_2 k Z_{jt} + c_j + s_{ijt} + sp_{ijkt} \]
This is essentially the same as Model 2, though this expanded model makes slightly fewer assumptions. In particular, Model 3 includes the additional parameters \(\gamma_0\) and \(\gamma_1\), where \(\gamma_0\) is the change from baseline to follow-up in the control arm and \(\gamma_{1}\) is the difference at baseline between control and treatment arms (we would expect this to be \(0\) in a randomized trial). \(\gamma_{2}\) is the difference in the change from baseline to follow-up between the two arms. In Model 2, we essentially make the assumption that both \(\gamma_0 = 0\) and \(\gamma_1=0\), which is probably true on average in a randomized trial with no secular trend between baseline and follow-up measurements (and is certainly true in our simulated data generation process). In this case, under the assumption of randomization and no within-period secular trend, \(\gamma_2\) should be equivalent to \(\gamma\) in Model 2.
fit_3 <- lmer(y ~ t + k * Z - 1 + (1|id:site) + (1|site), data = dd)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| t | |||
| 1 | -0.92 | -2.1, 0.23 | 0.11 |
| 2 | 2.6 | 1.5, 3.8 | <0.001 |
| 3 | 4.9 | 3.7, 6.1 | <0.001 |
| 4 | 7.9 | 6.5, 9.2 | <0.001 |
| 5 | 11 | 9.2, 12 | <0.001 |
| k | 0.20 | -0.12, 0.52 | 0.2 |
| Z | 0.38 | -0.57, 1.3 | 0.4 |
| k * Z | 0.83 | 0.38, 1.3 | <0.001 |
| id:site.sd__(Intercept) | 6.5 | ||
| site.sd__(Intercept) | 2.1 | ||
| Residual.sd__Observation | 4.5 |
The notable difference between the the Model 2 and Model 3 estimates is that the width of the confidence interval for the treatment effect estimate is considerably larger in Model 3. We will see how this plays out in the power estimates down below.
Model 4: ANCOVA
The next model is an ANCOVA model that adjusts each follow-up outcome \(Y_1\) with the observed baseline measurement \(Y_0.\) Because we have only a single outcome per subject, the subject-specific effect \(sp_{ijkt}\) disappears, and \(s_{ijt}\) is now individual subject-level noise.
\[ Y_{ijt} = \alpha_t + \beta Y_0 + \gamma Z_{jt} + c_j + s_{ijt} \]
dd_b <- dd[k ==0, .(id, y0 = y)]
dd_f <- dd[k ==1, ]
dd <- merge(dd_f, dd_b, by = "id")
fit_4 <- lmer(y ~ t + y0 + Z - 1 + (1|site), data = dd)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| t | |||
| 1 | -0.11 | -0.66, 0.44 | 0.7 |
| 2 | 1.1 | 0.54, 1.7 | <0.001 |
| 3 | 1.5 | 0.85, 2.2 | <0.001 |
| 4 | 2.9 | 2.1, 3.7 | <0.001 |
| 5 | 3.9 | 2.9, 4.8 | <0.001 |
| y0 | 0.69 | 0.67, 0.72 | <0.001 |
| Z | 0.74 | 0.06, 1.4 | 0.033 |
| site.sd__(Intercept) | 0.64 | ||
| Residual.sd__Observation | 5.8 |
Model 5: Change as outcome
The final model considers the change from baseline to follow-up (\(D_{ijt} = Y_{ij1t} - Y_{ij0t}\)) as the outcome of interest:
\[ D_{ijt} = \alpha_t + \gamma Z_{jt} + c_j + s_{ijt} \]
dd[, d := y - y0]
fit_5 <- lmer(d ~ t + Z - 1 + (1|site), data = dd)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| t | |||
| 1 | 0.17 | -0.35, 0.69 | 0.5 |
| 2 | 0.33 | -0.21, 0.88 | 0.2 |
| 3 | -0.04 | -0.66, 0.58 | >0.9 |
| 4 | 0.55 | -0.17, 1.3 | 0.13 |
| 5 | 0.63 | -0.22, 1.5 | 0.15 |
| Z | 0.58 | -0.09, 1.3 | 0.087 |
| site.sd__(Intercept) | 0.26 | ||
| Residual.sd__Observation | 6.3 |
Power estimates
The ultimate goal of simulating data under different scenarios is to compare how efficiently different modeling assumptions estimate the treatment effect. In frequentist terms, if we assume a specific effect size, which model will lead us to the “correct” inference most often? Or putting it more technically, which model has the most statistical power?
By repeatedly generate data sets, we can estimate the parameters using each of the models and compare the overall proportion of data sets where the observed p-value is less than 0.05 to evaluate the power of each modeling approach. We have generated data under a range of effect size and time trend assumptions, as well as under the different random effect assumptions to see if relative power changes across different sets of assumptions.
The simulations were conducted under a range of sample size assumptions (we assumed between 12 and 60 clusters) as well as two different time trends. (See the last section of the addendum for example code used for the power analysis.) Power was estimated for each set of assumptions using 1500 data sets.
First up is Scenario 1:
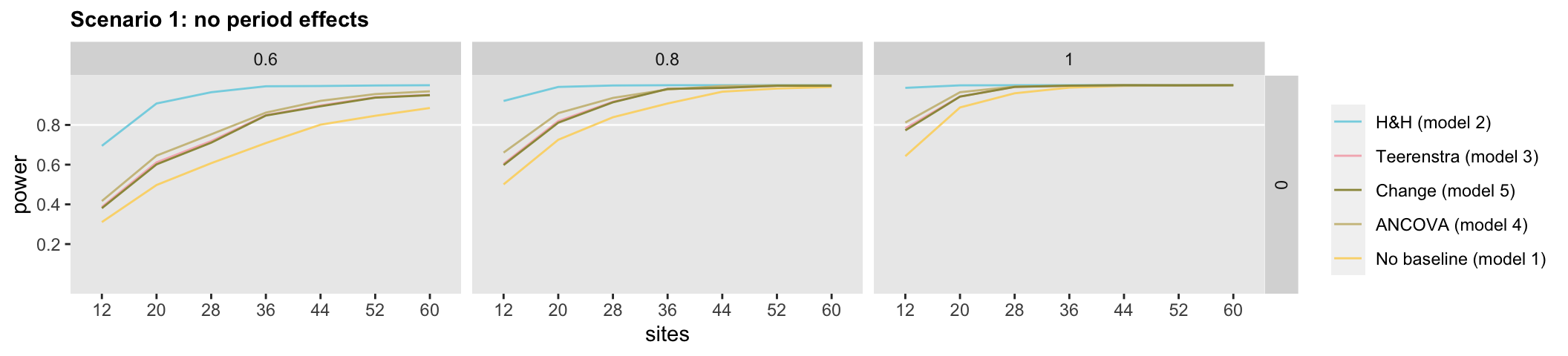
The curves in the figures show estimated power under a range of effect size (the columns of plots), time trends (the rows of plots) and sample size assumptions (the x-axes). In the case without any fixed or random period effects, there really is no difference between Models 3, 4, and 5; power appears to be consistent under the different scenarios. Model 2, the Hussey & Hughes model for baseline and follow-up measures, has the most power; this is not surprising, given that the model has an embedded set of simplifying assumptions relative to Model 3 (see above). On the flip side, if those assumptions are violated, the Model 3 estimates for the treatment effect may be biased, so it is not the obvious choice. On the other end of the spectrum, Model 1 that ignores the baseline measures provides the least power; it seems pretty clear that if the two measurements are available, it would be unwise to throw out one of them.
The relative weakness of Model 1 and relative strength (though potential bias) of Model 2 persist in the remaining two scenarios (below), so the interesting question is how the remaining three models fare. In the second scenario, where there are fixed period effects but no random period effects, differences emerge. Model 3, the difference in change or Teerenstra model, appears to have more power than the ANCOVA or change models across all effect sizes and secular trends.
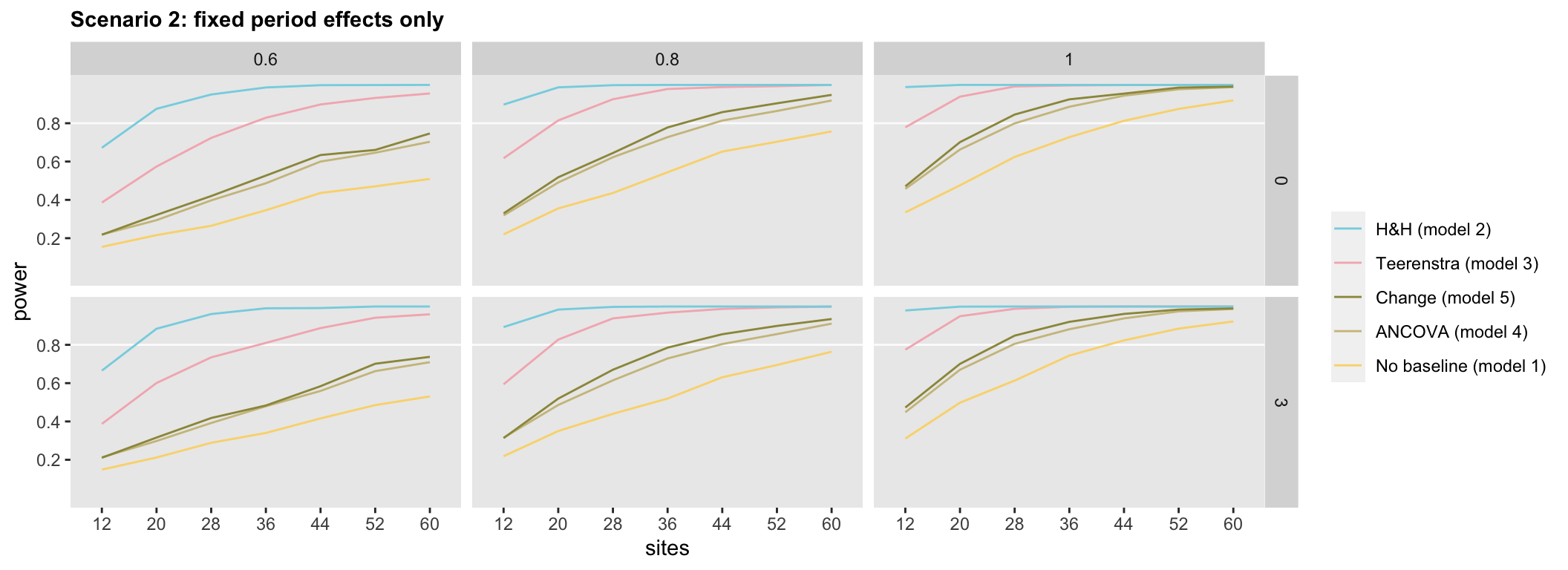
In Scenario 3, where we have both fixed and random period effects, the general ordering of the models appears similar to the ranking in Scenario 2. However, Model 5, the change model appears, surprisingly, slightly superior to Model 4, the ANCOVA model.
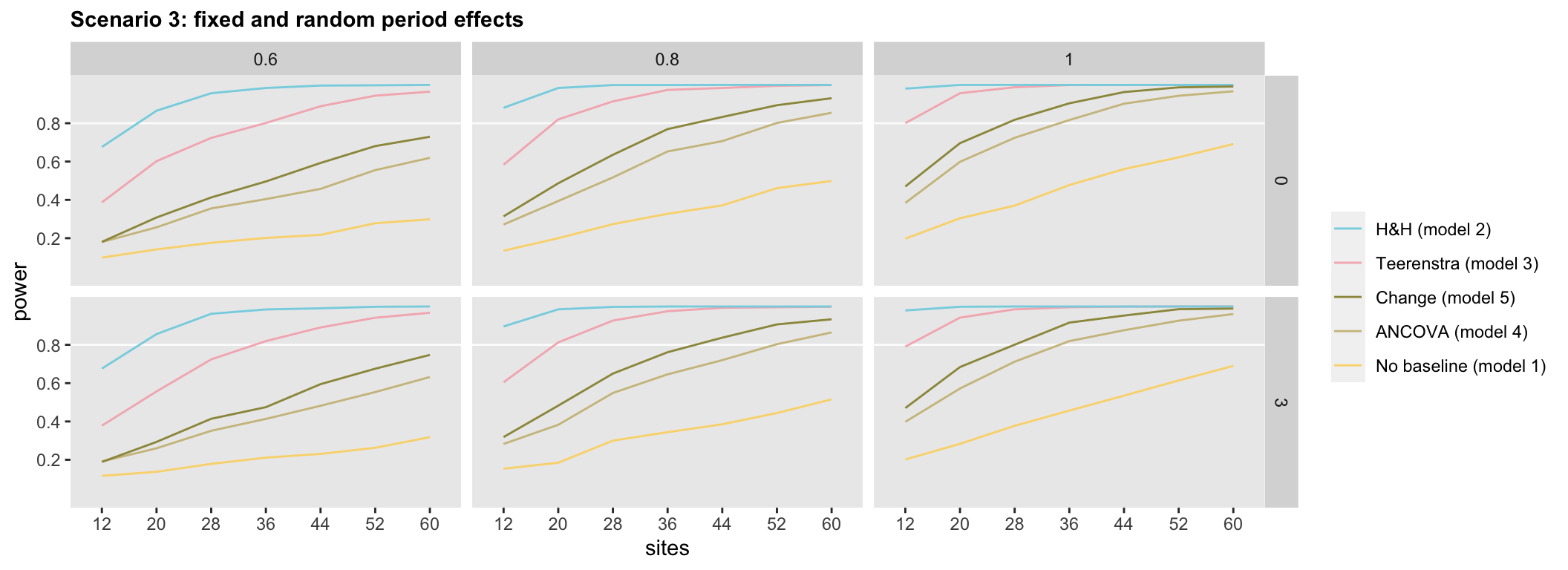
Back in the real world, of course, we do not know the true data generation process. It seems pretty clear that if we can make the assumptions that \(\gamma_0\) and \(\gamma_1 = 0\), then Model 2 appears to be the way to go. However, if we want to be careful not to introduce bias, Model 3 might preferred.
The important thing to note is that statistical power translates directly to sample size. If we are interested in achieving 80% power, we can see how the number of required clusters is reduced as we move leftward across the horizontal white white lines in the plots, from Model 1 to Models 4 & 5 to Model 3 and then to Model 2. This is the design effect in action.
Of course, these conclusions are based on the specific data generating assumptions of the simulations. More general guidelines will require the formal derivation of design effects of the different models under the various scenarios. That is the next step.
References:
Hussey, Michael A., and James P. Hughes. “Design and analysis of stepped wedge cluster randomized trials.” Contemporary clinical trials 28, no. 2 (2007): 182-191.
Teerenstra, Steven, Sandra Eldridge, Maud Graff, Esther de Hoop, and George F. Borm. “A simple sample size formula for analysis of covariance in cluster randomized trials.” Statistics in medicine 31, no. 20 (2012): 2169-2178.
Support:
This work was supported in part by the National Institute on Aging (NIA) of the National Institutes of Health under Award Number U54AG063546, which funds the NIA IMbedded Pragmatic Alzheimer’s Disease and AD-Related Dementias Clinical Trials Collaboratory (NIA IMPACT Collaboratory). The author, a member of the Design and Statistics Core, was the sole writer of this blog post and has no conflicts. The content is solely the responsibility of the author and does not necessarily represent the official views of the National Institutes of Health.
Addendum
(A) General data generation code: function base_sw
base_sw <- function(effect, trend, nsites, nwaves, nperiods, n, s_c, s_cp, s_s, s_sp) {
# define the cluster and subject level effects
defC <- defData(varname = "c", formula = 0, variance = "..s_c")
defCP <- defDataAdd(varname = "c.p", formula = 0, variance = "..s_cp")
defS <- defDataAdd(varname = "s", formula = 0, variance = "..s_s")
defSP <- defDataAdd(varname = "y",
formula = "..trend * s_per + ..effect * Z * k + c + c.p + s",
variance = "..s_sp"
)
# generate clusters
dsite <- genData(nsites, defC, id = "site")
# generate cluster-period data
dper <- addPeriods(dsite, nPeriods = nperiods, idvars = "site",
timeid = "s_time", perName = "s_per")
dper <- addColumns(defCP, dper)
# make treatment assignments
dsw <- trtStepWedge(dper, "site", nWaves = nwaves, lenWaves = 1,
startPer = 1, perName = "s_per",
grpName = "Z")
# generate individual level data within each cluster
dpat <- genCluster(dper, cLevelVar = "s_time",
numIndsVar = n, level1ID = "id")
dpat <- addColumns(defS, dpat)
# generate two observation periods for each subject - baseline and follow-up
dpat <- addPeriods(dpat, nPeriods=2, idvars="id", timeid="p_time", perName="k")
# merge subjects with stepped wedge assignments and generate outcome
setkey(dpat, "s_time", "site", "s_per", "id")
dsw[, c("c", "c.p") := NULL]
setkey(dsw, "s_time", "site", "s_per")
dpat <- merge(dpat, dsw)
setkey(dpat, "id", "k")
dpat <- addColumns(defSP, dpat)
}(B) Model 3 under Scenarios 1 and 3
The modeling examples above were based on Scenario 2 assumptions. Here is Model 3 under Scenarios 1 and 3. (The other models would be described and implemented in similar fashion.)
Scenario 1
In Scenario 1, there are no fixed or random period effects, so there is a constant intercept \(\alpha\) for each period, rather than period-specific intercepts \(\alpha_t\), and there is no site-period random effect \(cp_{jt}\):
\[ Y_{ijkt} = \alpha + \gamma_0 k + \gamma_1 Z_{jk} + \gamma_2 k Z_{jk} + c_j + s_{ijt} + sp_{ijkt} \]
dd <- base_sw(effect = 1, trend = 0, 20, 4, 5, 30, 6, 0, 44, 20)
fit_1a <- lmer(y ~ k * Z + (1|id:site) + (1|site), data = dd)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| k | 0.24 | -0.09, 0.56 | 0.2 |
| Z | 0.51 | -0.11, 1.1 | 0.11 |
| k * Z | 0.47 | 0.01, 0.93 | 0.044 |
| id:site.sd__(Intercept) | 6.5 | ||
| site.sd__(Intercept) | 2.1 | ||
| Residual.sd__Observation | 4.5 |
Scenario 3
Scenario 3 includes both fixed and random period effects, so we have \(\alpha_t\) and \(cp_{jt}\).
\[ Y_{ijkt} = \alpha_t + \gamma_0 k + \gamma_1 Z_{jk} + \gamma_2 k Z_{jk} + c_j + cp_{jt} + s_{ijt} + sp_{ijkt} \]
dd <- base_sw(effect = 1, trend = 3, 20, 4, 5, 30, 4, 2, 44, 20)
dd[, t := factor(s_per, labels = c(1, 2, 3, 4, 5))]
fit_2a <- lmer(y ~ t + k * Z - 1 + (1|id:site) + (1|s_time:site) + (1|site),
data = dd)| Characteristic | Beta | 95% CI | p-value |
|---|---|---|---|
| t | |||
| 1 | -0.89 | -2.1, 0.36 | 0.2 |
| 2 | 2.6 | 1.3, 3.9 | <0.001 |
| 3 | 6.0 | 4.6, 7.4 | <0.001 |
| 4 | 9.6 | 8.0, 11 | <0.001 |
| 5 | 13 | 11, 15 | <0.001 |
| k | 0.07 | -0.25, 0.38 | 0.7 |
| Z | -1.5 | -2.9, -0.15 | 0.030 |
| k * Z | 1.0 | 0.50, 1.4 | <0.001 |
| id:site.sd__(Intercept) | 6.8 | ||
| s_time:site.sd__(Intercept) | 1.4 | ||
| site.sd__(Intercept) | 1.9 | ||
| Residual.sd__Observation | 4.4 |
(C) Code to estimate statistical power
Here is the code to estimate statistical power of each model under a range of parameter assumptions, assuming Scenario 2 with fixed period effects. The estimation was conducted using a high performance computing cluster, because the replication process is computationally intensive.
library(simstudy)
library(data.table)
library(slurmR)
s_single_rep <- function(argsvec) {
list2env(as.list(argsvec), envir = environment())
dd <- base_sw(effect, trend, sites, waves, periods, npat, 6, 0, 44, 20)
# Model 1
d_std <- dd[k == 1]
fit_1 <- lmer( y ~ t + Z - 1 + (1|site), data = d_std)
pval_1 <- coef(summary(fit_1))["Z", "Pr(>|t|)"]
# Model 2
fit_2 <- lmer(y ~ t + k:Z - 1 + (1|id:site) + (1|site), data = dd)
pval_2 <- coef(summary(fit_2))["k:Z", "Pr(>|t|)"]
# Model 3
fit_3 <- lmer(y ~ t + k * Z - 1 + (1|id:site) + (1|site), data = dd)
pval_3 <- coef(summary(fit_3))["k:Z", "Pr(>|t|)"]
# Model 4
dd_b <- dd[p_fu == 0, .(id, y0 = y)]
dd_f <- dd[p_fu == 1, ]
dd_a <- merge(dd_f, dd_b, by = "id")
fit_4 <- lmer(y ~ t + k * Z - 1 + (1|id:site) + (1|site), data = dd_a)
pval_4 <- coef(summary(fit_4))["Z", "Pr(>|t|)"]
# Model 5
dd[, d := y - y0]
fit_5 <- lmer(d ~ t + Z - 1 + (1|site), data = dd)
pval_5 <- coef(summary(fit_5))["Z", "Pr(>|t|)"]
###
data.table(pval_1, pval_2, pval_3, pval_4, pval_5)
}
s_replicate <- function(argsvec) {
model_results <- rbindlist(
parallel::mclapply(
X = 1:1500,
FUN = function(x) s_single_rep(argsvec),
mc.cores = 8)
)
#--- summary statistics ---#
power <- model_results[, .(pval_1 = mean(pval_1 <= 0.05),
pval_2 = mean(pval_2 <= 0.05),
pval_3 = mean(pval_3 <= 0.05),
pval_4 = mean(pval_4 <= 0.05),
pval_5 = mean(pval_5 <= 0.05)
)]
summary_stats <- data.table(t(argsvec), power)
return(summary_stats) # summary_stats is a data.table}
}
### Set simulation parameters
scenario_list <- function(...) {
argmat <- expand.grid(...)
return(asplit(argmat, MARGIN = 1))
}
effect <- 1
trend <- c(0, 3)
sites <- c(12, 20, 28, 36, 44, 52, 60)
npat <- 30
waves <- 4
periods = 5
scenarios <- scenario_list(effect = effect, trend = trend,
sites = sites, npat=npat, waves = waves, periods = periods)
### Execute simulation
job <- Slurm_lapply(
X = scenarios,
FUN = s_replicate,
njobs = min(length(scenarios), 90L),
mc.cores = 8L,
job_name = "i_swt",
tmp_path = "/gpfs/.../scratch",
plan = "wait",
sbatch_opt = list(time = "03:00:00", partition = "cpu_short"),
export = c("simple_swt", "base_swt", "s_single_rep"),
overwrite = TRUE
)
### Gather and save results
res <- Slurm_collect(job)
save(res, file = "/gpfs/.../res.rda")