When we are trying to assess the effect of an exposure or intervention on an outcome, confounding is an ever-present threat to our ability to draw the proper conclusions. My goal (starting here and continuing in upcoming posts) is to think a bit about how to characterize confounding in a way that makes it possible to literally see why improperly estimating intervention effects might lead to bias.
Confounding, potential outcomes, and causal effects
Typically, we think of a confounder as a factor that influences both exposure and outcome. If we ignore the confounding factor in estimating the effect of an exposure, we can easily over- or underestimate the size of the effect due to the exposure. If sicker patients are more likely than healthier patients to take a particular drug, the relatively poor outcomes of those who took the drug may be due to the initial health status rather than the drug.
A slightly different view of confounding is tied to the more conceptual framework of potential outcomes, which I wrote a bit about earlier. A potential outcome is the outcome we would observe if an individual were subjected to a particular exposure. We may or may not observe the potential outcome - this depends on the actual exposure. (To simplify things here, I will assume we are interested only in two different exposures.) \(Y_0\) and \(Y_1\) represent the potential outcomes for an individual with and without exposure, respectively. We observe \(Y_0\) if the individual is not exposed, and \(Y_1\) if she is.
The causal effect of the exposure for the individual \(i\) can be defined as \(Y_{1i} - Y_{0i}\). If we can observe each individual in both states (with and without the exposure) long enough to measure the outcome \(Y\), we are observing both potential outcomes and can measure the causal effect for each individual. Averaging across all individuals in the sample provides an estimate the population average causal effect. (Think of a crossover or N-of-1 study.)
Unfortunately, in the real world, it is rarely feasible to expose an individual to multiple conditions. Instead, we use one group as a proxy for the other. For example, the control group represents what would have happened to the exposed group had the exposed group not been exposed. This approach only makes sense if the control group is identical in every way to the exposure group (except for the exposure, of course.)
Our goal is to compare the distribution of outcomes for the control group with the exposed group. We often simplify this comparison by looking at the means of each distribution. The average causal effect (across all individuals) can be written as \(E(Y_1 - Y_0)\), where \(E()\) is the expectation or average. In reality, we cannot directly measure this since only one potential outcome is observed for each individual.
Using the following logic, we might be able to convince ourselves that we can use observed measurements to estimate unobservable average causal effects. First, we can say \(E(Y_1 - Y_0) = E(Y_1) - E(Y_0)\), because expectation is linear. Next, it seems fairly reasonable to say that \(E(Y_1 | A = 1) = E(Y | A = 1)\), where \(A=1\) for exposure, \(A=0\) for control. In words, this states that the average potential outcome of exposure for the exposed group is the same as what we actually observe for the exposed group (this is the consistency assumption in causal inference theory). Along the same lines, \(E(Y_0 | A = 0) = E(Y | A = 0)\). Finally, if we can say that \(E(Y_1) = E(Y_1 | A = 1)\) - the potential outcome of exposure for everyone is equal to the potential outcome of exposure for those exposed - then we can say that \(E(Y_1) = E(Y | A = 1)\) (the potential outcome with exposure for everyone is the same as the observed outcome for the exposed. Similarly, we can make the same argument to conclude that \(E(Y_0) = E(Y | A = 0)\). At the end of this train of logic, we conclude that we can estimate \(E(Y_1 - Y_0)\) using observed data only: \(E(Y | A = 1) - E(Y | A = 0)\).
This nice logic fails if \(E(Y_1) \ne E(Y | A = 1)\) and/or \(E(Y_0) \ne E(Y | A = 0)\). That is, this nice logic fails when there is confounding.
This is all a very long-winded way of saying that confounding arises when the distributions of potential outcomes for the population are different from those distributions for the subgroups we are using for analysis. For example, if the potential outcome under exposure for the population as a whole (\(Y_1\)) differs from the observed outcome for the subgroup that was exposed (\(Y|A=1\)), or the potential outcome without exposure for the entire population (\(Y_0\)) differs from the observed outcome for the subgroup that was not exposed (\(Y|A=0\)), any estimates of population level causal effects using observed data will be biased.
However, if we can find a factor \(L\) (or factors) where
\[ \begin{aligned} P(Y_1 | L=l) &= P(Y | A = 1 \text{ and } L=l) \\ P(Y_0 | L=l) &= P(Y | A = 0 \text{ and } L=l) \end{aligned} \] both hold for all levels or values of \(L\), we can remove confounding (and get unbiased estimates of the causal effect) by “controlling” for \(L\). In some cases, the causal effect we measure will be conditional on \(L\), sometimes it will be a population-wide average (or marginal) causal effect, and sometimes it will be both.
What confounding looks like …
The easiest way to illustrate the population/subgroup contrast is to generate data from a process that includes confounding. In this first example, the outcome is continuous, and is a function of both the exposure (\(A\)) and a covariate (\(L\)). For each individual, we can generate both potential outcomes \(Y_0\) and \(Y_1\). (Note that both potential outcomes share the same individual level noise term \(e\) - this is not a necessary assumption.) This way, we can “know” the true population, or marginal causal effect of exposure. The observed outcome \(Y\) is determined by the exposure status. For the purposes of plotting a smooth density curve, we generate a very large sample - 2 million.
library(simstudy)
defC <- defData(varname = "e", formula = 0, variance = 2,
dist = "normal")
defC <- defData(defC, varname = "L", formula = 0.4,
dist = "binary")
defC <- defData(defC, varname = "Y0", formula = "1 + 4*L + e",
dist = "nonrandom")
defC <- defData(defC, varname = "Y1", formula = "5 + 4*L + e",
dist = "nonrandom")
defC <- defData(defC, varname = "A", formula = "0.3 + 0.3 * L",
dist = "binary")
defC <- defData(defC, varname = "Y", formula = "1 + 4*A + 4*L + e",
dist = "nonrandom")
set.seed(2017)
dtC <- genData(n = 2000000, defC)
dtC[1:5]## id e L Y0 Y1 A Y
## 1: 1 2.02826718 1 7.0282672 11.028267 1 11.0282672
## 2: 2 -0.10930734 0 0.8906927 4.890693 0 0.8906927
## 3: 3 1.04529790 0 2.0452979 6.045298 0 2.0452979
## 4: 4 -2.48704266 1 2.5129573 6.512957 1 6.5129573
## 5: 5 -0.09874778 0 0.9012522 4.901252 0 0.9012522Feel free to skip over this code - I am just including in case anyone finds it useful to see how I generated the following series of annotated density curves:
library(ggplot2)
getDensity <- function(vector, weights = NULL) {
if (!is.vector(vector)) stop("Not a vector!")
if (is.null(weights)) {
avg <- mean(vector)
} else {
avg <- weighted.mean(vector, weights)
}
close <- min(which(avg < density(vector)$x))
x <- density(vector)$x[close]
if (is.null(weights)) {
y = density(vector)$y[close]
} else {
y = density(vector, weights = weights)$y[close]
}
return(data.table(x = x, y = y))
}
plotDens <- function(dtx, var, xPrefix, title, textL = NULL, weighted = FALSE) {
dt <- copy(dtx)
if (weighted) {
dt[, nIPW := IPW/sum(IPW)]
dMarginal <- getDensity(dt[, get(var)], weights = dt$nIPW)
} else {
dMarginal <- getDensity(dt[, get(var)])
}
d0 <- getDensity(dt[L==0, get(var)])
d1 <- getDensity(dt[L==1, get(var)])
dline <- rbind(d0, dMarginal, d1)
brk <- round(dline$x, 1)
p <- ggplot(aes(x=get(var)), data=dt) +
geom_density(data=dt[L==0], fill = "#ce682f", alpha = .4) +
geom_density(data=dt[L==1], fill = "#96ce2f", alpha = .4)
if (weighted) {
p <- p + geom_density(aes(weight = nIPW),
fill = "#2f46ce", alpha = .8)
} else p <- p + geom_density(fill = "#2f46ce", alpha = .8)
p <- p + geom_segment(data = dline, aes(x = x, xend = x,
y = 0, yend = y),
size = .7, color = "white", lty=3) +
annotate(geom="text", x = 12.5, y = .24,
label = title, size = 5, fontface = 2) +
scale_x_continuous(limits = c(-2, 15),
breaks = brk,
name = paste(xPrefix, var)) +
theme(panel.grid = element_blank(),
axis.text.x = element_text(size = 12),
axis.title.x = element_text(size = 13)
)
if (!is.null(textL)) {
p <- p +
annotate(geom = "text", x = textL[1], y = textL[2],
label = "L=0", size = 4, fontface = 2) +
annotate(geom = "text", x = textL[3], y = textL[4],
label="L=1", size = 4, fontface = 2) +
annotate(geom = "text", x = textL[5], y = textL[6],
label="Population distribution", size = 4, fontface = 2)
}
return(p)
}library(gridExtra)
grid.arrange(plotDens(dtC, "Y0", "Potential outcome", "Full\npopulation",
c(1, .24, 5, .22, 2.6, .06)),
plotDens(dtC[A==0], "Y", "Observed", "Unexposed\nonly"),
plotDens(dtC, "Y1", "Potential outcome", "Full\npopulation"),
plotDens(dtC[A==1], "Y", "Observed", "Exposed\nonly"),
nrow = 2
)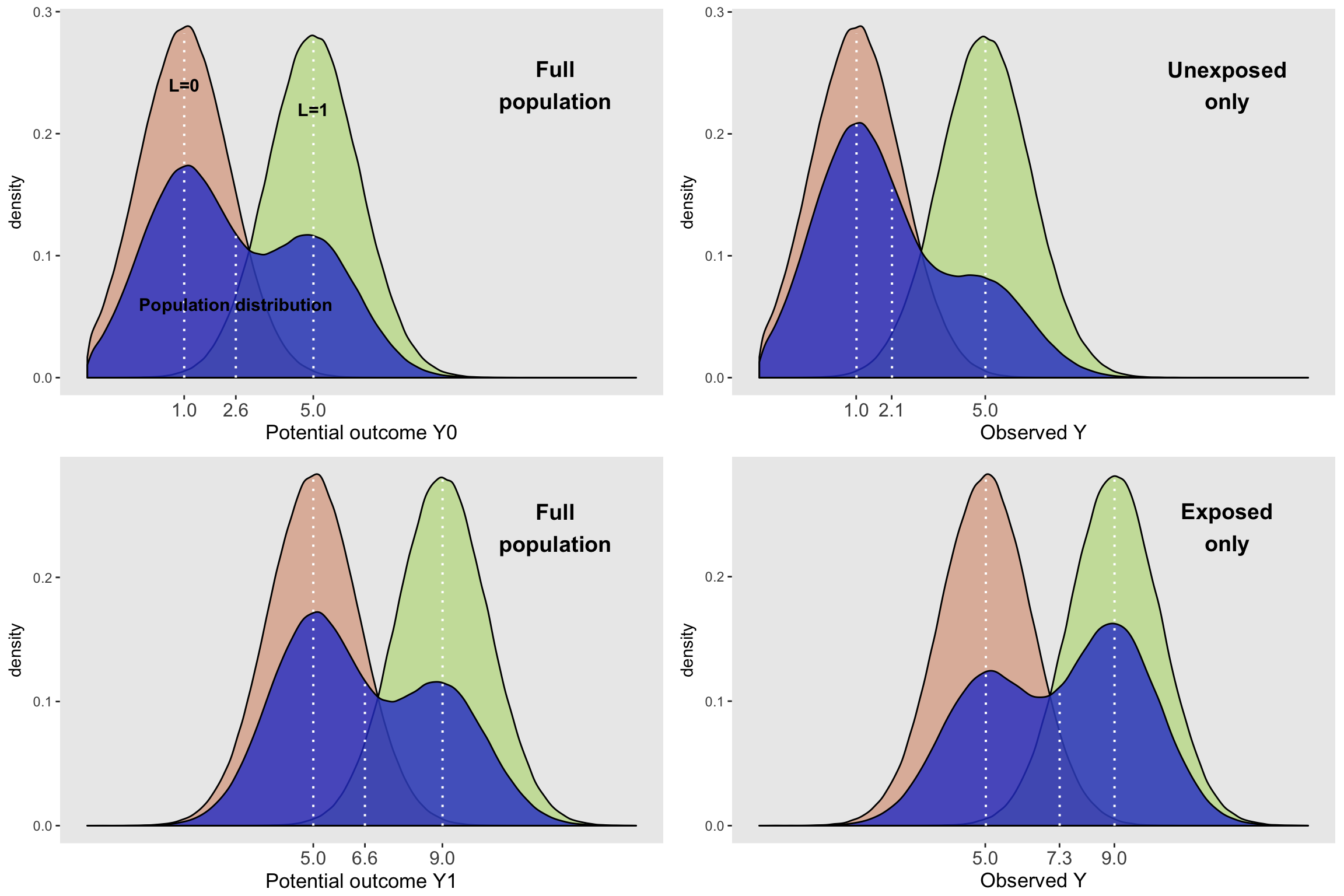
Looking at the various plots, we can see a few interesting things. The density curves on the left represent the entire population. The conditional distributions of the potential outcomes at the population level are all normally distributed, with means that depend on the exposure and covariate \(L\). We can also see that the population-wide distribution of \(Y_0\) and \(Y_1\) (in blue) are non-symmetrically shaped, because they are a mixture of the conditional normal distributions, weighted by the proportion of each level of \(L\). Since the proportions for the top and bottom plots are in fact the population proportion, the population-level density curves for \(Y_0\) and \(Y_1\) are similarly shaped, with less mass on the higher end, because individuals are less likely to have an \(L\) value of 1:
dtC[, .(propLis1 = mean(L))]## propLis1
## 1: 0.399822The shape of the marginal distribution of \(Y_1\) is identical to \(Y_0\) (in this case, because that is the way I generated the data), but shifted to the right by an amount equal to the causal effect. The conditional effect sizes are 4, as is the population or marginal effect size.
The subgroup plots on the right are a different story. In this case, the distributions of \(L\) vary across the exposed and unexposed groups:
dtC[, .(propLis1 = mean(L)), keyby = A]## A propLis1
## 1: 0 0.2757937
## 2: 1 0.5711685So, even though the distributions of (observed) \(Y\) conditional on \(L\) are identical to their potential outcome counterparts in the whole population - for example, \(P(Y | A=0 \text{ and } L = 1) = P(Y_0 | L = 1)\) - the marginal distributions of \(Y\) are quite different for the exposed and unexposed. For example, \(P(Y | A = 0) \ne P(Y_0)\). This is directly due to the fact that the mixing weights (the proportions of \(L\)) are different for each of the groups. In the unexposed group, about 28% have \(L=1\), but for the exposed group, about 57% do. Using the subgroup data only, the conditional effect sizes are still 4 (comparing mean outcomes \(Y\) within each level of \(L\)). However the difference in means between the marginal distributions of each subgroup is about 5.2 (calculated by 7.3 - 2.1). This is confounding.
No confounding
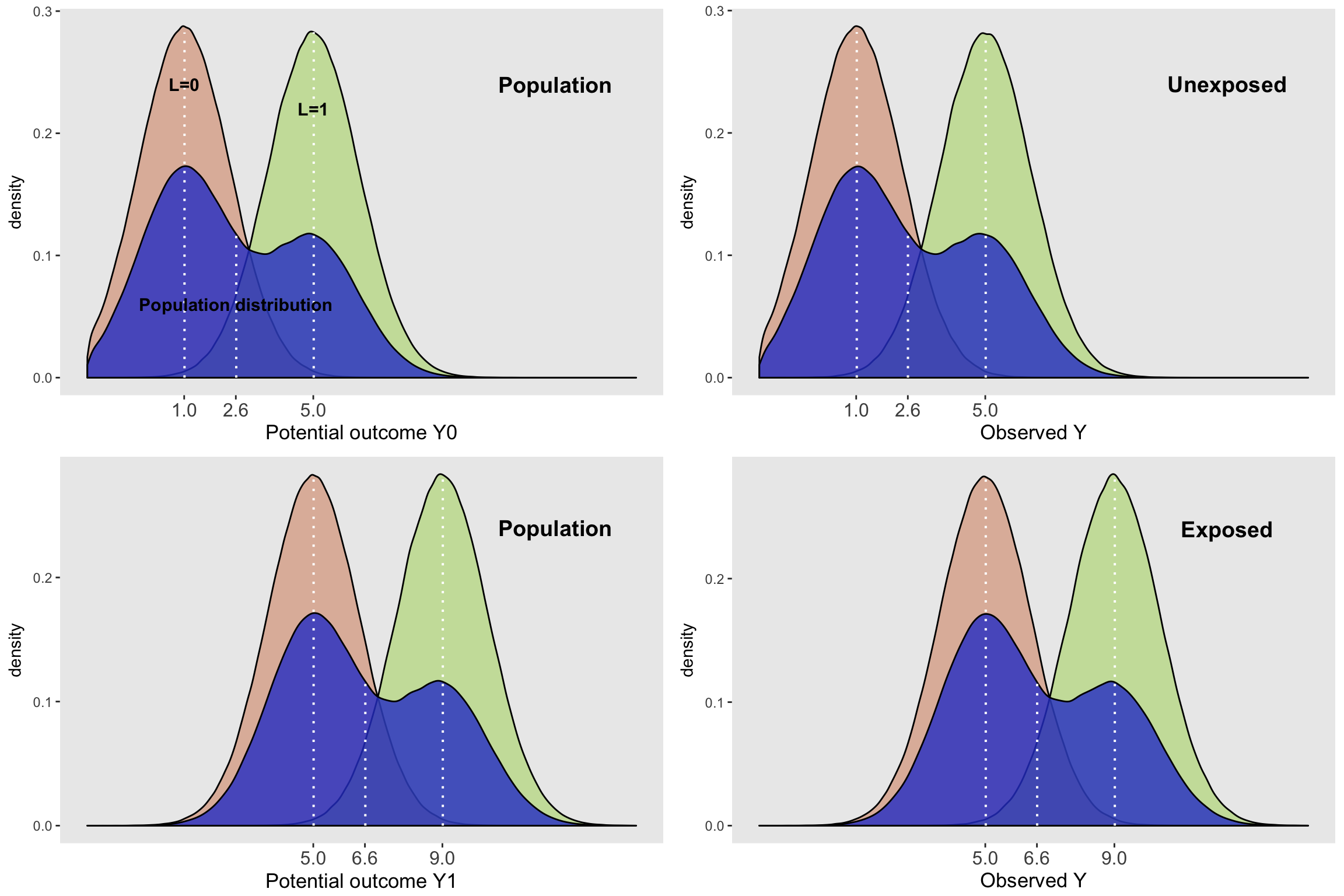
Just so we can see that when the covariate \(L\) has nothing to do with the probability of exposure, the marginal distributions of the subgroups do in fact look like their population-level potential outcome marginal distributions:
defC <- updateDef(defC, "A", newformula = 0.5) # change data generation
dtC <- genData(n = 2000000, defC)
dtC[, .(propLis1 = mean(L)), keyby = A] # subgroup proportions## A propLis1
## 1: 0 0.4006499
## 2: 1 0.3987437dtC[, .(propLis1 = mean(L))] # population/marginal props## propLis1
## 1: 0.3996975grid.arrange(plotDens(dtC, "Y0", "Potential outcome", "Population",
c(1, .24, 5, .22, 2.6, .06)),
plotDens(dtC[A==0], "Y", "Observed", "Unexposed"),
plotDens(dtC, "Y1", "Potential outcome", "Population"),
plotDens(dtC[A==1], "Y", "Observed", "Exposed"),
nrow = 2
)
Estimation of causal effects (now with confounding)
Generating a smaller data set, we estimate the causal effects using simple calculations and linear regression:
library(broom)
# change back to confounding
defC <- updateDef(defC, "A", newformula = ".3 + .3 * L")
dtC <- genData(2500, defC)The true average (marginal) causal effect from the average difference in potential outcomes for the entire population:
dtC[, mean(Y1 - Y0)]## [1] 4And the true average causal effects conditional on the covariate \(L\):
dtC[, mean(Y1 - Y0), keyby = L]## L V1
## 1: 0 4
## 2: 1 4If we try to estimate the marginal causal effect by using a regression model that does not include \(L\), we run into problems. The estimate of 5.2 we see below is the same biased estimate we saw in the plot above. This model is reporting the differences of the means (across both levels of \(L\)) for the two subgroups, which we know (because we saw) are not the same as the potential outcome distributions in the population due to different proportions of \(L\) in each subgroup:
tidy(lm(Y ~ A, data = dtC))## term estimate std.error statistic p.value
## 1 (Intercept) 2.027132 0.06012997 33.71251 1.116211e-205
## 2 A 5.241004 0.09386145 55.83766 0.000000e+00If we estimate a model that conditions on \(L\), the estimates are on target because in the context of normal linear regression without interaction terms, conditional effects are the same as marginal effects (when confounding has been removed, or think of the comparisons being made within the orange groups and green groups in the fist set of plots above, not within the purple groups):
tidy(lm(Y ~ A + L , data = dtC))## term estimate std.error statistic p.value
## 1 (Intercept) 0.9178849 0.03936553 23.31697 5.809202e-109
## 2 A 4.0968358 0.05835709 70.20288 0.000000e+00
## 3 L 3.9589109 0.05862583 67.52844 0.000000e+00Inverse probability weighting (IPW)
What follows briefly here is just a sneak preview of IPW (without any real explanation), which is one way to recover the marginal mean using observed data with confounding. For now, I am ignoring the question of why you might be interested in knowing the marginal effect when the conditional effect estimate provides the same information. Suffice it to say that the conditional effect is not always the same as the marginal effect (think of data generating processes that include interactions or non-linear relationships), and sometimes the marginal effect estimate may the best that we can do, or at least that we can do easily.
If we weight each individual observation by the inverse probability of exposure, we can remove confounding and estimate the marginal effect of exposure on the outcome. Here is a quick simulation example.
After generating the dataset (the same large one we started out with so you can compare) we estimate the probability of exposure \(P(A=1 | L)\), assuming that we know the correct exposure model. This is definitely a questionable assumption, but in this case, we actually do. Once the model has been fit, we assign the predicted probability to each individual based on her value of \(L\).
set.seed(2017)
dtC <- genData(2000000, defC)
exposureModel <- glm(A ~ L, data = dtC, family = "binomial")
tidy(exposureModel)## term estimate std.error statistic p.value
## 1 (Intercept) -0.847190 0.001991708 -425.3584 0
## 2 L 1.252043 0.003029343 413.3053 0dtC[, pA := predict(exposureModel, type = "response")]The IPW is not based exactly on \(P(A=1 | L)\) (which is commonly used in propensity score analysis), but rather, the probability of the actual exposure at each level of \(L\): \(P(A=a | L)\), where \(a\in(0,1)\):
# Define two new columns
defC2 <- defDataAdd(varname = "pA_actual",
formula = "A * pA + (1-A) * (1-pA)",
dist = "nonrandom")
defC2 <- defDataAdd(defC2, varname = "IPW",
formula = "1/pA_actual",
dist = "nonrandom")
# Add weights
dtC <- addColumns(defC2, dtC)
round(dtC[1:5], 2)## id e L Y0 Y1 A Y pA pA_actual IPW
## 1: 1 2.03 1 7.03 11.03 1 11.03 0.6 0.6 1.67
## 2: 2 -0.11 0 0.89 4.89 0 0.89 0.3 0.7 1.43
## 3: 3 1.05 0 2.05 6.05 0 2.05 0.3 0.7 1.43
## 4: 4 -2.49 1 2.51 6.51 1 6.51 0.6 0.6 1.67
## 5: 5 -0.10 0 0.90 4.90 0 0.90 0.3 0.7 1.43To estimate the marginal effect on the log-odds scale, we use function lm again, but with weights specified by IPW. The true value of the marginal effect of exposure (based on the population-wide potential outcomes) was 4.0. I know I am repeating myself here, but first I am providing the biased estimate that we get when we ignore covariate \(L\) to convince you that the relationship between exposure and outcome is indeed confounded:
tidy(lm(Y ~ A , data = dtC)) ## term estimate std.error statistic p.value
## 1 (Intercept) 2.101021 0.002176711 965.2275 0
## 2 A 5.184133 0.003359132 1543.2956 0And now, with the simple addition of the weights but still not including \(L\) in the model, our weighted estimate of the marginal effect is spot on (but with such a large sample size, this is not so surprising):
tidy(lm(Y ~ A , data = dtC, weights = IPW)) ## term estimate std.error statistic p.value
## 1 (Intercept) 2.596769 0.002416072 1074.789 0
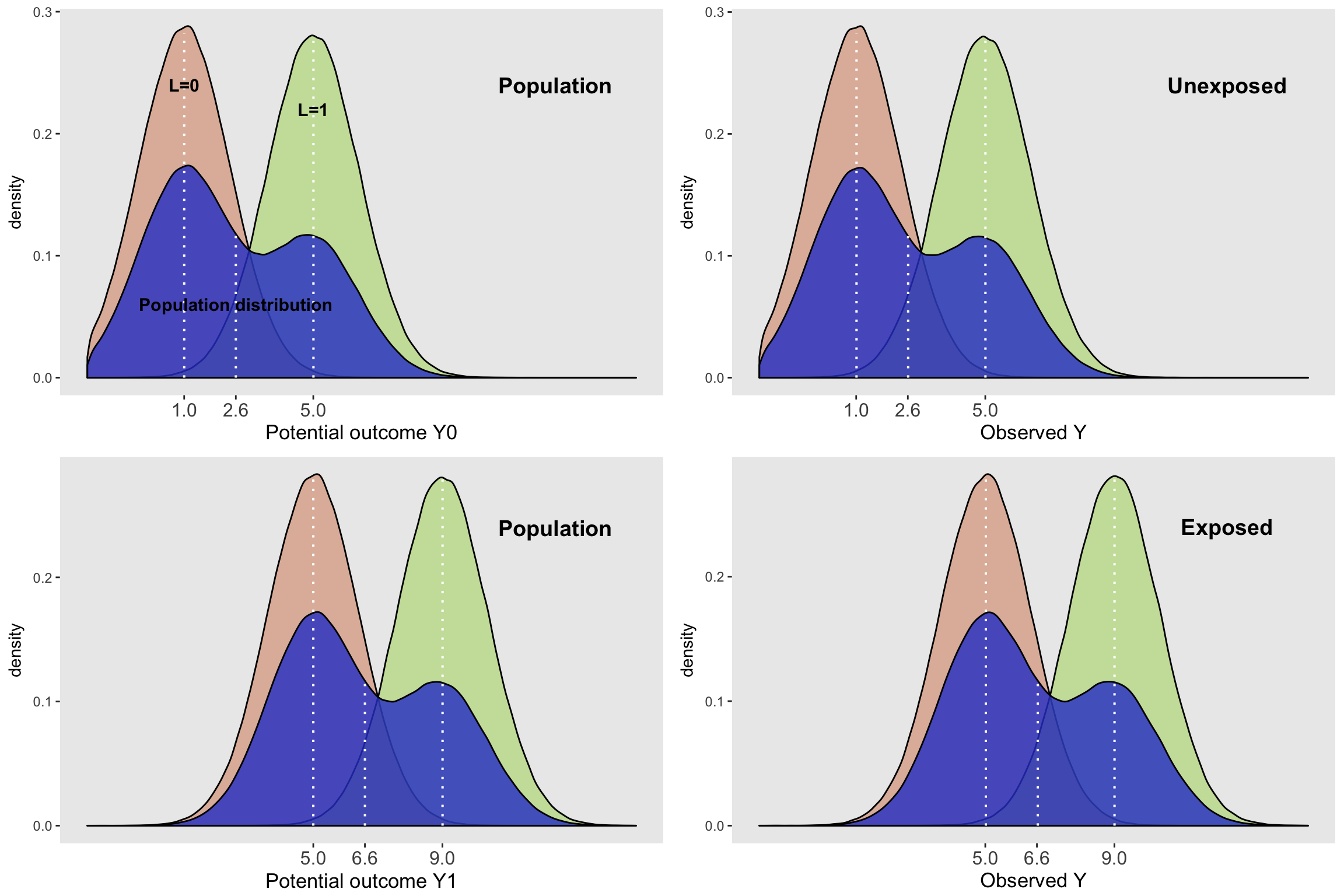
## 2 A 4.003122 0.003416842 1171.585 0And finally, here is a plot of the IPW-adjusted density. You might think I am just showing you the plots for the unconfounded data again, but you can see from the code (and I haven’t hidden anything) that I am still using the data set with confounding. In particular, you can see that I am calling the routine plotDens with weights.
grid.arrange(plotDens(dtC, "Y0", "Potential outcome", "Population",
c(1, .24, 5, .22, 2.6, .06)),
plotDens(dtC[A==0], "Y", "Observed", "Unexposed",
weighted = TRUE),
plotDens(dtC, "Y1", "Potential outcome", "Population"),
plotDens(dtC[A==1], "Y", "Observed", "Exposed",
weighted = TRUE),
nrow = 2
)
As I mentioned, I hope to write more on IPW, and marginal structural models, which make good use of this methodology to estimate effects that can be challenging to get a handle on.