Continuing the discussion on cumulative odds models I started last time, I want to investigate a solution I always assumed would help mitigate a failure to meet the proportional odds assumption. I’ve believed if there is a large number of categories and the relative cumulative odds between two groups don’t appear proportional across all categorical levels, then a reasonable approach is to reduce the number of categories. In other words, fewer categories translates to proportional odds. I’m not sure what led me to this conclusion, but in this post I’ve created some simulations that seem to throw cold water on that idea.
When the odds are proportional
I think it is illustrative to go through a base case where the odds are actually proportional. This will allow me to introduce the data generation and visualization that I’m using to explore this issue. I am showing a lot of code here, because I think it is useful to see how it is possible to visualize cumulative odds data and the model estimates.
The first function genDT generates a data set with two treatment arms and an ordinal outcome. genOrdCat uses a base set of probabilities for the control arm, and the experimental arm probabilities are generated under an assumption of proportional cumulative odds (see the previous post for more details on what cumulative odds are and what the model is).
library(simstudy)
library(data.table)
genDT <- function(nobs, baseprobs, defA) {
dT <- genData(nobs)
dT <- trtAssign(dT, grpName = "rx")
dT <- addColumns(defA, dT)
dT <- genOrdCat(dT, adjVar = "z", baseprobs, catVar = "r")
dT[]
}In this case, I’ve set the base probabilities for an ordinal outcome of 8 categories. The log of the cumulative odds ratio comparing experimental arm to control is 1.0 (and is parameterized as -1.0). In this case, the proportional odds ratio should be about 2.7.
baseprobs <- c(0.05, 0.10, 0.15, 0.25, .20, 0.15, .05, .05)
defA <- defDataAdd(varname = "z", formula = "-1.0 * rx", dist = "nonrandom")
set.seed(29672) # 19779
dT.prop <- genDT(200, baseprobs, defA)Calculation of the observed cumulative odds ratio at each response level doesn’t provide an entirely clear picture about proportionality, but the sample size is relatively small given the number of categories.
codds <- function(cat, dx) {
dcodds <- dx[, .(codds = mean(as.numeric(r) <= cat)/mean(as.numeric(r) > cat)),
keyby = rx]
round(dcodds[rx == 1, codds] / dcodds[rx==0, codds], 2)
}
sapply(1:7, function(x) codds(x, dT.prop))## [1] 1.48 3.81 3.12 1.83 2.05 3.59 2.02A visual assessment
An excellent way to assess proportionality is to do a visual comparison of the observed cumulative probabilities with the estimated cumulative probabilities from the cumulative odds model that makes the assumption of proportional odds.
I’ve written three functions that help facilitate this comparison. getCumProbs converts the parameter estimates of cumulative odds from the model to estimates of cumulative probabilities.
getCumProbs <- function(coefs) {
cumprob0 <- data.table(
cumprob = c(1/(1 + exp(-coefs[which(rownames(coefs) != "rx")])), 1),
r = factor(1 : nrow(coefs)),
rx = 0
)
cumprob1 <- data.table(
cumprob = c(1/(1 + exp(-coefs[which(rownames(coefs) != "rx")] +
coefs["rx", 1])), 1),
r = factor(1 : nrow(coefs)),
rx = 1
)
rbind(cumprob0, cumprob1)[]
}The function bootCumProb provides a single bootstrap from the data so that we can visualize the uncertainty of the estimated cumulative probabilities. In this procedure, a random sample is drawn (with replacement) from the data set, a clm model is fit, and the cumulative odds are converted to cumulative probabilities.
library(ordinal)
bootCumProb <- function(bootid, dx) {
sampid <- dx[, .(srow = sample(.I, replace = TRUE)), keyby = rx][, srow]
dtBoot <- dx[sampid,]
bootFit <- clm(r ~ rx, data = dtBoot)
bcoefs <- coef(summary(bootFit))
bcumProbs <- getCumProbs(bcoefs)
bcumProbs[, bootid := bootid]
bcumProbs[]
}The third function fitPlot fits a clm model to the original data set, collects the bootstrapped estimates, calculates the observed cumulative probabilities, converts the estimated odds to estimated probabilities, and generates a plot of the observed data, the model fit, and the bootstrap estimates.
library(ggplot2)
library(paletteer)
fitPlot <- function(dx) {
clmFit <- clm(r ~ rx, data = dx)
coefs <- coef(summary(clmFit))
bootProbs <- rbindlist(lapply(1:500, function(x) bootCumProb(x, dx)))
cumObsProbs <- dx[, .N, keyby = .(rx, r)]
cumObsProbs[, cumprob := cumsum(N)/sum(N) , keyby = rx]
cumModProbs <- getCumProbs(coefs)
ggplot(data = cumObsProbs, aes(x = r, y = cumprob , color = factor(rx))) +
geom_line(data = cumModProbs, alpha = 1, aes(group=rx)) +
geom_line(data = bootProbs, alpha = .01,
aes(group = interaction(rx, bootid))) +
geom_point() +
ylab("cumulative probability") +
xlab("ordinal category") +
theme(panel.grid = element_blank(),
legend.position = "none") +
scale_color_paletteer_d("jcolors::pal6")
}Here is a plot based on the original data set of 200 observations. The observed values are quite close to the modeled estimates, and well within the range of the bootstrap estimates.
fitPlot(dT.prop)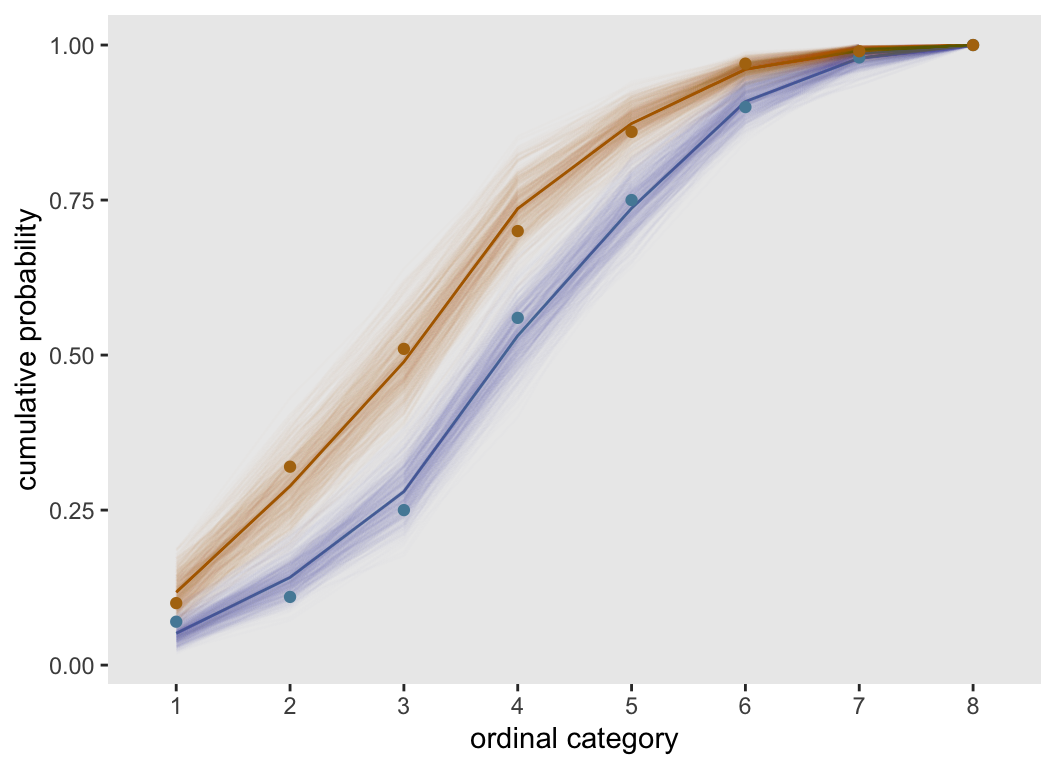
Collapsing the categories
Continuing with the same data set, let’s see what happens when we collapse categories together. I’ve written a function collapseCat that takes a list of vectors of categories that are to be combined and returns a new, modified data set.
collapseCat <- function(dold, collapse) {
dx <- copy(dold)
for (i in 1:length(collapse)) {
dx[r %in% collapse[[i]], r:= min(collapse[[i]])]
}
dx[, r := factor(r)]
dx[, r := factor(r, labels = c(1:length(levels(r))))]
dx[]
}Here is the distribution of the original data set:
dT.prop[, table(rx, r)]## r
## rx 1 2 3 4 5 6 7 8
## 0 7 4 14 31 19 15 8 2
## 1 10 22 19 19 16 11 2 1And if we combine categories 1, 2, and 3 together, as well as 7 and 8, here is the resulting distribution based on the remaining five categories. Here’s a quick check to see that the categories were properly combined:
collapse <- list(c(1,2,3), c(7,8))
collapseCat(dT.prop, collapse)[, table(rx, r)]## r
## rx 1 2 3 4 5
## 0 25 31 19 15 10
## 1 51 19 16 11 3If we create four modified data sets based on different combinations of groups, we can fit models and plot the cumulative probabilities for all for of them. In all cases the proportional odds assumption still seems pretty reasonable.
collapse <- list(list(c(3, 4), c(6, 7)),
list(c(1,2,3), c(7,8)),
list(c(1,2,3), c(4, 5), c(7,8)),
list(c(1,2), c(3, 4, 5), c(6, 7, 8))
)
dC.prop <- lapply(collapse, function(x) collapseCat(dT.prop, x))
cplots <- lapply(dC.prop, function(x) fitPlot(x))
gridExtra::grid.arrange(grobs = cplots, nrow = 2)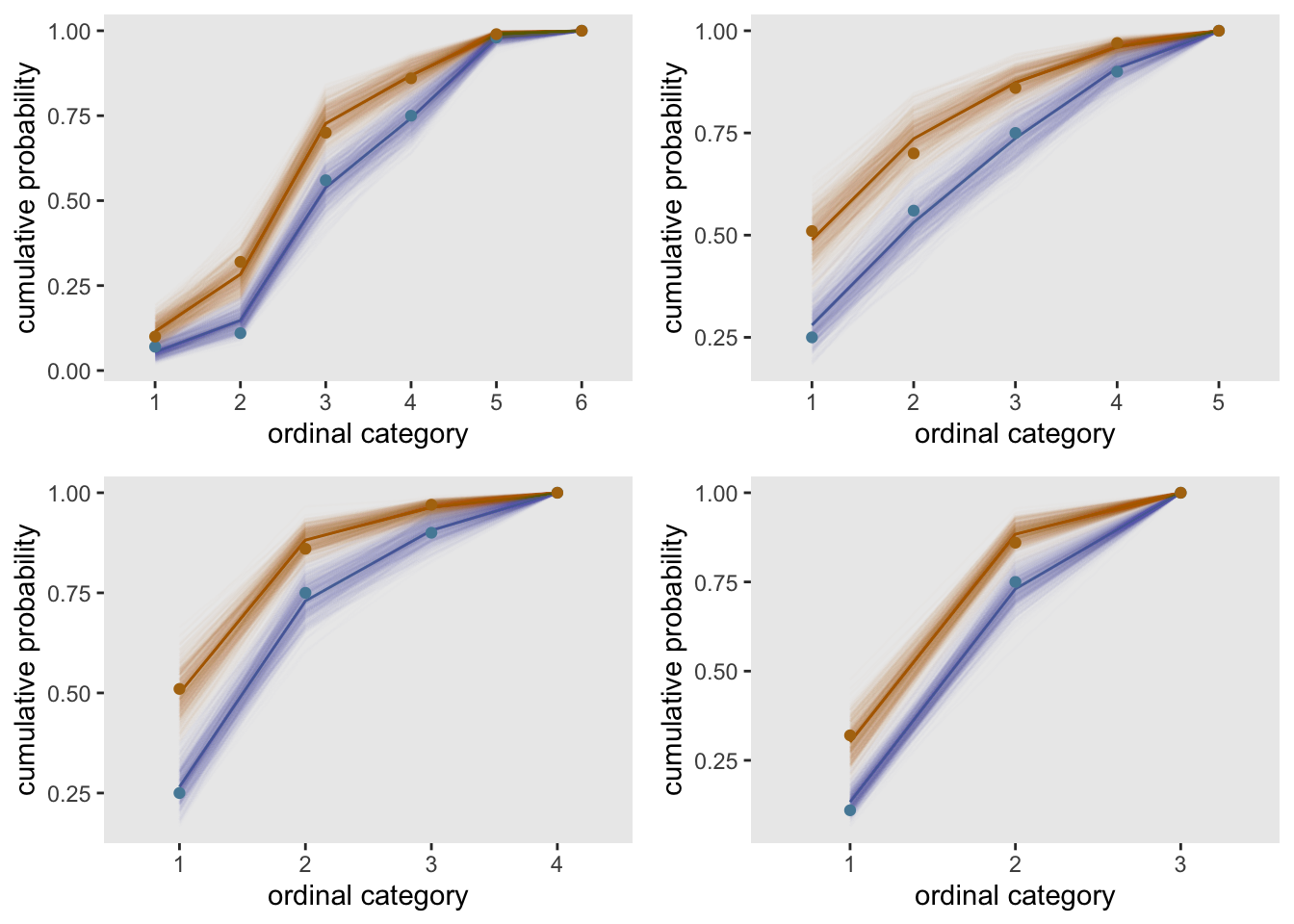
Non-proportional cumulative odds
That was all just a set-up to explore what happens in the case of non-proportional odds. To do that, there’s just one more function to add - we need to generate data that does not assume proportional cumulative odds. I use the rdirichlet in the gtools package to generate values between 0 and 1, which sum to 1. The key here is that there is no pattern in the data - so that the ratio of the cumulative odds will not be constant.
genDTnon <- function(nobs, ncat) {
ps <- gtools::rdirichlet(2, rep(2, ncat))
p0 <- paste(ps[1, -ncat], collapse = ";")
p1 <- paste(ps[2, -ncat], collapse = ";")
defc <- defCondition(condition = "rx == 0", formula = p0,
dist = "categorical")
defc <- defCondition(defc, condition = "rx == 1", formula = p1,
dist = "categorical")
dx <- genData(nobs)
dx <- trtAssign(dx, grpName = "rx")
dx <- addCondition(defc, dx, "r")
dx[, r := factor(r)]
dx[]
}Again, we generate a data set with 200 observations and an ordinal categorical outcome with 8 levels. The plot of the observed and estimated cumulative probabilities suggests that the proportional odds assumption is not a good one here. Some of the observed probabilities are quite far from the fitted lines, particularly at the low end of the ordinal scale. It may not be a disaster to to use a clm model here, but it is probably not a great idea.
dT.nonprop <- genDTnon(200, 8)
fitPlot(dT.nonprop)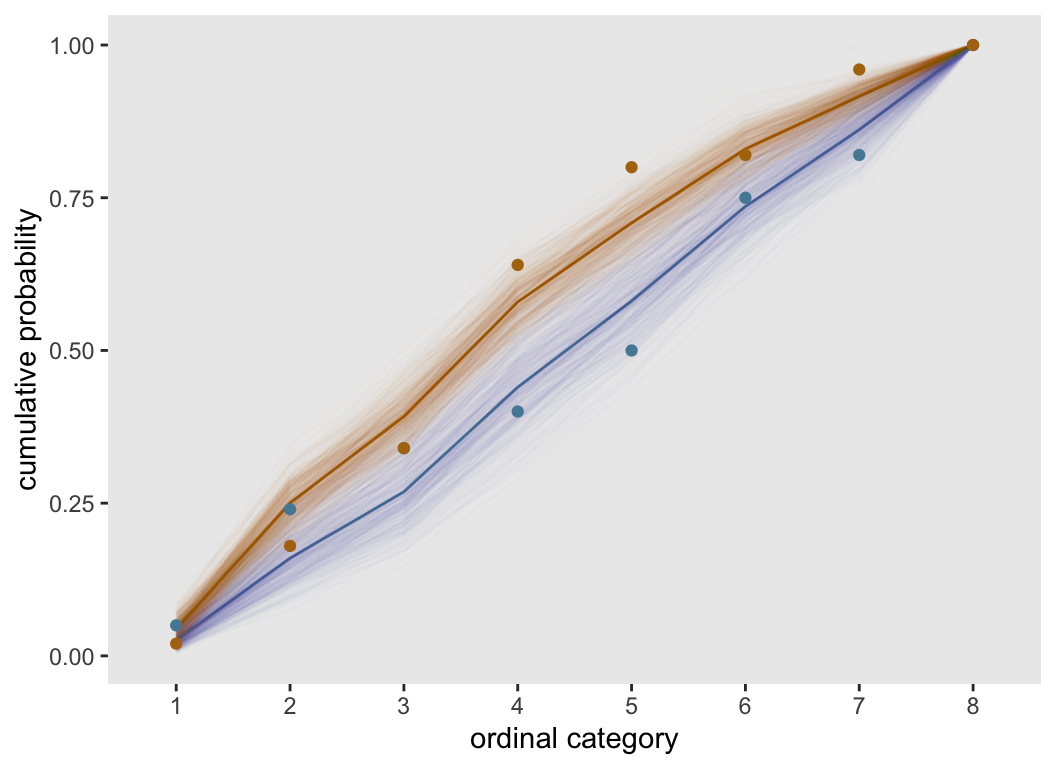
The question remains - if we reduce the number of categories does the assumption of proportional odds come into focus? The four scenarios shown here do not suggest much improvement. The observed data still fall outside or at the edge of the bootstrap bands for some levels in each case.
dC.nonprop <- lapply(collapse, function(x) collapseCat(dT.nonprop, x))
cplots <- lapply(dC.nonprop, function(x) fitPlot(x))
gridExtra::grid.arrange(grobs = cplots, nrow = 2)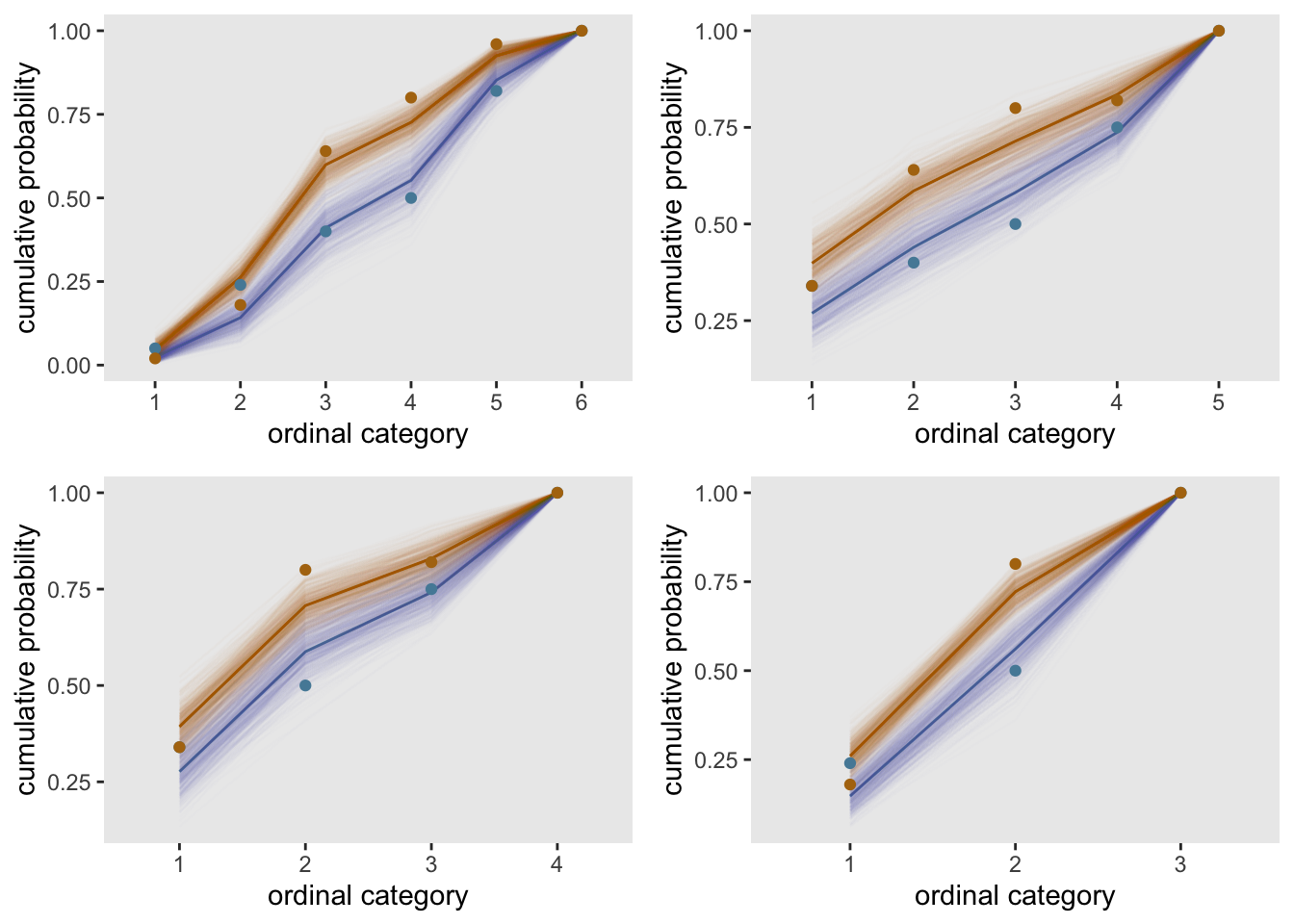
What should we do in this case? That is a tough question. The proportional odds model for the original data set with eight categories is probably just as reasonable as estimating a model using any of the combined data sets; there is no reason to think that any one of the alternatives with fewer categories will be an improvement. And, as we learned last time, we may actually lose power by collapsing some of the categories. So, it is probably best to analyze the data set using its original structure, and find the best model for that data set. Ultimately, that best model may need to relax the proportionality assumption; a post on that will need to be written another time.