Say we have an intervention that is assigned at a group or cluster level but the outcome is measured at an individual level (e.g. students in different schools, eyes on different individuals). And, say this outcome is binary; that is, something happens, or it doesn’t. (This is important, because none of this is true if the outcome is continuous and close to normally distributed.) If we want to measure the effect of the intervention - perhaps the risk difference, risk ratio, or odds ratio - it can really matter if we are interested in the marginal effect or the conditional effect, because they likely won’t be the same.
My aim is to show this through a couple of data simulations that allow us to see this visually.
First example
In the first scenario, I am going to use a causal inference framework that uses the idea that everyone has a potential outcome under one exposure (such as an intervention of some sort), and another potential outcome under a different exposure (such as treatment as usual or control). (I may discuss potential outcomes and causal inference in more detail in the future.) The potential outcome can be written with a superscript, lie \(Y^0\) or \(Y^1\).
To generate the data, I will use this simple model for each potential outcome: \[ log\left[\frac{P(Y^0_{ij})}{1-P(Y^0_{ij})}\right] = \gamma + \alpha_i\]
and \[ log\left[\frac{P(Y^1_{ij})}{1-P(Y^1_{ij})}\right] = \gamma + \alpha_i + \delta.\] \(\delta\) is the treatment effect and is constant across the clusters, on the log-odds scale. \(\alpha_i\) is the cluster specific effect for cluster \(i\). \(Y^a_{ij}\) is the potential outcome for individual \(j\) under exposure \(a\).
Now let’s generate some data and look at it:
# Define data
def1 <- defData(varname = "clustEff", formula = 0, variance = 2,
id = "cID")
def1 <- defData(def1, varname = "nInd", formula = 10000,
dist = "noZeroPoisson")
def2 <- defDataAdd(varname = "Y0", formula = "-1 + clustEff",
dist = "binary", link = "logit")
def2 <- defDataAdd(def2, varname = "Y1",
formula = "-1 + clustEff + 2",
dist = "binary", link = "logit")
options(width = 80)
def1## varname formula variance dist link
## 1: clustEff 0 2 normal identity
## 2: nInd 10000 0 noZeroPoisson identitydef2## varname formula variance dist link
## 1: Y0 -1 + clustEff 0 binary logit
## 2: Y1 -1 + clustEff + 2 0 binary logit# Generate cluster level data
set.seed(123)
dtC <- genData(n = 100, def1)
# Generate individual level data
dt <- genCluster(dtClust = dtC, cLevelVar = "cID", numIndsVar = "nInd",
level1ID = "id")
dt <- addColumns(def2, dt)Since we have repeated measurements for each cluster (the two potential outcomes), we can transform this into a “longitudinal” data set, though the periods are not time but different exposures.
dtLong <- addPeriods(dtName = dt, idvars = c("id","cID"),
nPeriods = 2,timevars = c("Y0","Y1"),
timevarName = "Y"
)When we look at the data visually, we get a hint that the marginal (or average) effect might not be the same as the conditional (cluster-specific) effects.
# Calculate average potential outcomes by exposure (which is called period)
dtMean <- dtLong[, .(Y = mean(Y)), keyby = .(period, cID)] # conditional mean
dtMMean <- dtLong[, .(Y = mean(Y)), keyby = .(period)] # marginal mean
dtMMean[, cID := 999]
ggplot(data = dtMean, aes(x=factor(period), y = Y, group= cID)) +
# geom_jitter(width= .25, color = "grey75") +
geom_line(color = "grey75", position=position_jitter(w=0.02, h=0.02)) +
geom_point(data=dtMMean) +
geom_line(data=dtMMean, size = 1, color = "red") +
ylab("Estimated cluster probability") +
scale_y_continuous(labels = scales::percent) +
theme(axis.title.x = element_blank()) +
my_theme()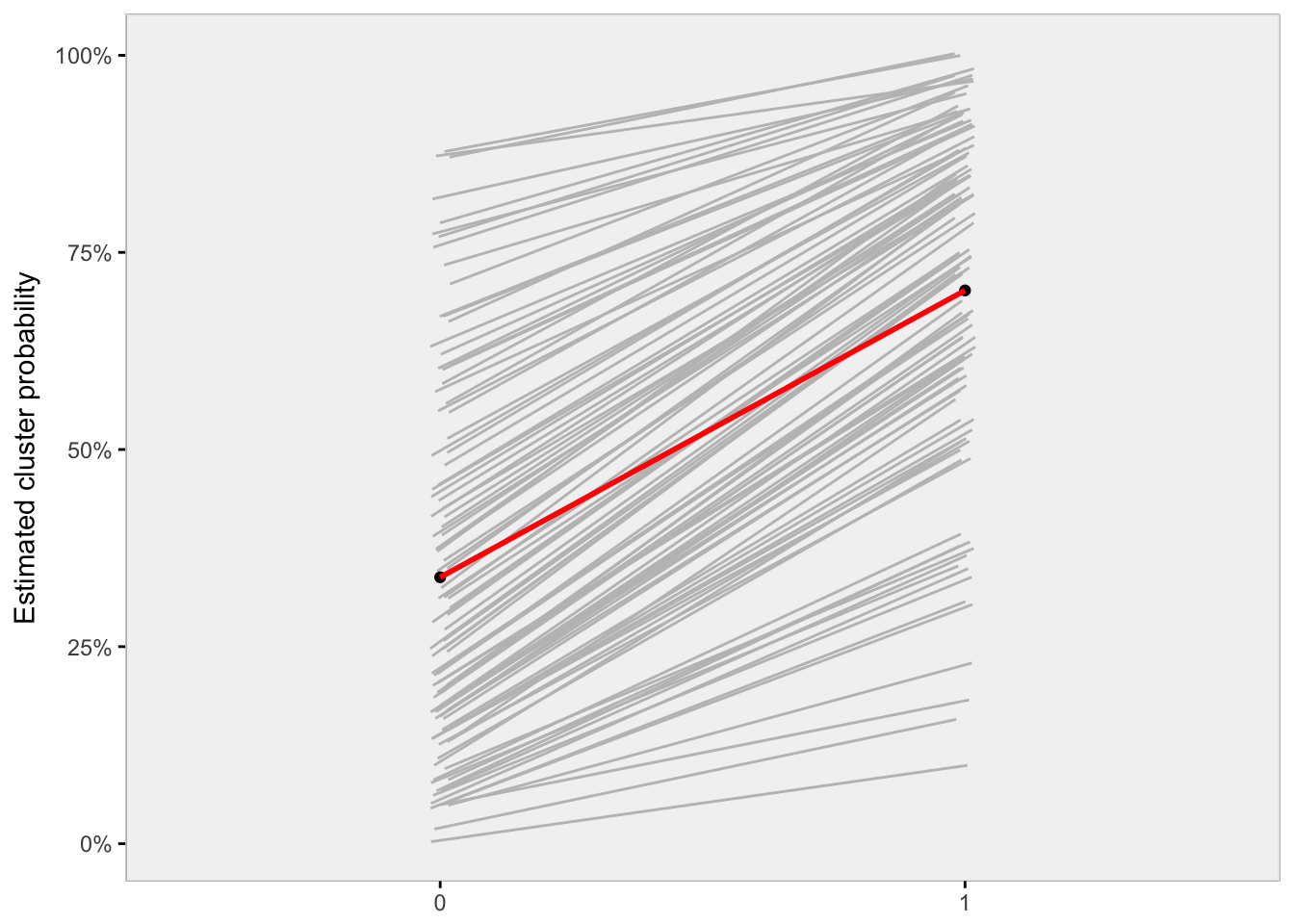
Looking at the plot, we see that the slopes of the grey lines - each representing the change in probability as a result of the exposure for each cluster - vary quite a bit. When the probability without exposure (\(Y^0\)) is particularly low or high, the absolute effect of the intervention is small (the slope is minimal). The slope or absolute effect increases when the starting probability is closer to 50%. The red line represents the averages of \(Y^0\) and \(Y^1\) across all individuals in all clusters. There is no reason to believe that the average slope of the grey lines is the same as the slope of the red line, which is slope of the averages. We will see that more clearly with the next data generation scenario.
Finally, if we look at cluster-specific effects of exposure, we see that on the risk difference scale (difference in probabilities), there is much variation, but on the log-odds ratio scale there is almost no variation. This is as it should be, because on the log-odds scale (which is how we generated the data), the difference between exposure and non-exposure is additive. On the probability scale, the difference is multiplicative. Here are some estimated differences for a sample of clusters:
dtChange <- dt[, .(Y0 = mean(Y0), Y1 = mean(Y1)), keyby = cID]
dtChange[, riskdiff := round(Y1 - Y0, 2)]
dtChange[, loratio := round( log( (Y1 / (1-Y1)) / (Y0 / (1-Y0) )), 2)]
dtChange[sample(1:100, 10, replace = F),
.(Y0 = round(Y0,2), Y1 = round(Y1,2), riskdiff, loratio),
keyby=cID]## cID Y0 Y1 riskdiff loratio
## 1: 18 0.02 0.14 0.12 1.95
## 2: 19 0.50 0.89 0.39 2.06
## 3: 22 0.22 0.67 0.45 1.97
## 4: 24 0.12 0.49 0.37 1.94
## 5: 30 0.69 0.94 0.26 2.00
## 6: 31 0.40 0.83 0.42 1.95
## 7: 34 0.56 0.90 0.35 1.99
## 8: 38 0.26 0.72 0.46 2.01
## 9: 72 0.01 0.09 0.08 1.97
## 10: 99 0.22 0.66 0.44 1.93Second example
This time around, we will add an additional individual level covariate that will help us visualize the difference a bit more clearly. Let us say that age is positively associated with increased probability in the outcome. (In this case, we measured age and then normalized it so that the mean age in the sample is 0.) And this time around, we are not going to use potential outcomes, but will randomly assign clusters to an intervention or treatment group.
This is the data generating model and the code:
\[ log\left[\frac{P(Y_{ij})}{1-P(Y_{ij})}\right] = \gamma + \alpha_j + \beta_1*Trt_j + \beta_2*Age_i\]
def1 <- defData(varname = "clustEff", formula = 0, variance = 2, id = "cID")
def1 <- defData(def1, varname = "nInd", formula = 100, dist = "noZeroPoisson")
# Each individual now has a measured age
def2 <- defDataAdd(varname = "age", formula = 0, variance = 2)
def2 <- defDataAdd(def2, varname = "Y",
formula = "-4 + clustEff + 2*trt + 2*age",
dist = "binary", link = "logit")
# Generate cluster level data
dtC <- genData(200, def1)
dtC <- trtAssign(dtC, grpName = "trt") #
# Generate individual level data
dt <- genCluster(dtClust = dtC, cLevelVar = "cID", numIndsVar = "nInd",
level1ID = "id")
dt <- addColumns(def2, dt)By fitting a conditional model (generalized linear mixed effects model) and a marginal model (we should fit a generalized estimating equation model to get the proper standard error estimates, but will estimate a generalized linear model, because the GEE model does not have a “predict” option in R; the point estimates for both marginal models should be quite close), we can see that indeed the conditional and marginal averages can be quite different.
glmerFit1 <- glmer(Y ~ trt + age + (1 | cID), data = dt, family="binomial")
glmFit1 <- glm(Y ~ trt + age, family = binomial, data = dt)## Intercept Trt Age
## conditional model -3.82 1.99 2.01
## marginal model -2.97 1.60 1.54Now, we’d like to visualize how the conditional and marginal treatment effects diverge. We can use the model estimates from the conditional model to predict probabilities for each cluster, age, and treatment group. (These will appear as grey lines in the plots below). We can also predict marginal probabilities from the marginal model based on age and treatment group while ignoring cluster. (These marginal estimates appear as red lines.) Finally, we can predict probability of outcomes for the conditional model also based on age and treatment group alone, but fixed at a mythical cluster whose random effect is 0. (These “average” conditional estimates appear as black lines.)
newCond <- expand.grid(cID = unique(dt$cID), age=seq(-4, 4, by =.1))
newCond0 <- data.table(trt = 0, newCond)
newCond1 <- data.table(trt = 1, newCond)
newMarg0 <- data.table(trt = 0, age = seq(-4, 4, by = .1))
newMarg1 <- data.table(trt = 1, age = seq(-4, 4, by = .1))
newCond0[, pCond0 := predict(glmerFit1, newCond0, type = "response")]
newCond1[, pCond1 := predict(glmerFit1, newCond1, type = "response")]
newMarg0[, pMarg0 := predict(glmFit1, newMarg0, type = "response")]
newMarg0[, pCAvg0 := predict(glmerFit1, newMarg0[,c(1,2)],
re.form = NA, type="response")]
newMarg1[, pMarg1 := predict(glmFit1, newMarg1, type = "response")]
newMarg1[, pCAvg1 := predict(glmerFit1, newMarg1[,c(1,2)],
re.form = NA, type="response")]
dtAvg <- data.table(age = newMarg1$age,
avgMarg = newMarg1$pMarg1 - newMarg0$pMarg0,
avgCond = newMarg1$pCAvg1 - newMarg0$pCAvg0
)
p1 <- ggplot(aes(x = age, y = pCond1), data=newCond1) +
geom_line(color="grey", aes(group = cID)) +
geom_line(data=newMarg1, aes(x = age, y = pMarg1), color = "red", size = 1) +
geom_line(data=newMarg1, aes(x = age, y = pCAvg1), color = "black", size = 1) +
ggtitle("Treatment group") +
xlab("Age") +
ylab("Probability") +
my_theme()
p0 <- ggplot(aes(x = age, y = pCond0), data=newCond0) +
geom_line(color="grey", aes(group = cID)) +
geom_line(data=newMarg0, aes(x = age, y = pMarg0), color = "red", size = 1) +
geom_line(data=newMarg0, aes(x = age, y = pCAvg0), color = "black", size = 1) +
ggtitle("Control group") +
xlab("Age") +
ylab("Probability") +
my_theme()
pdiff <- ggplot(data = dtAvg) +
geom_line(aes(x = age, y = avgMarg), color = "red", size = 1) +
geom_line(aes(x = age, y = avgCond), color = "black", size = 1) +
ggtitle("Risk difference") +
xlab("Age") +
ylab("Probability") +
my_theme()
grid.arrange(p1, p0, pdiff)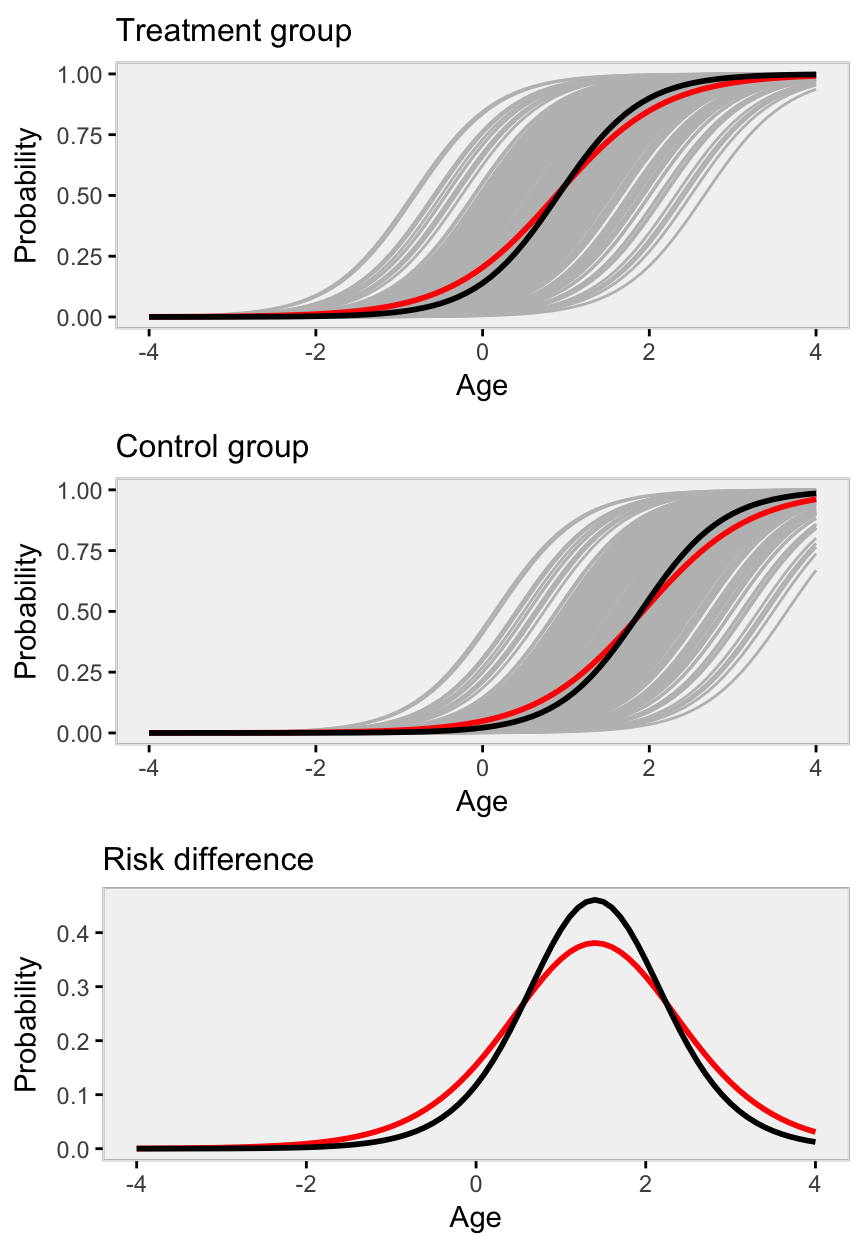
We see pretty clearly across all ages that the marginal and conditional estimates of average treatment differences differ quite dramatically.
Below are point estimates and plots for data generated with very little variance across clusters, that is \(var(\alpha_i)\) is close to 0. (We change this in the simulation by setting def1 <- defData(varname = "clustEff", formula = 0, variance = 0.05, id = "cID").)
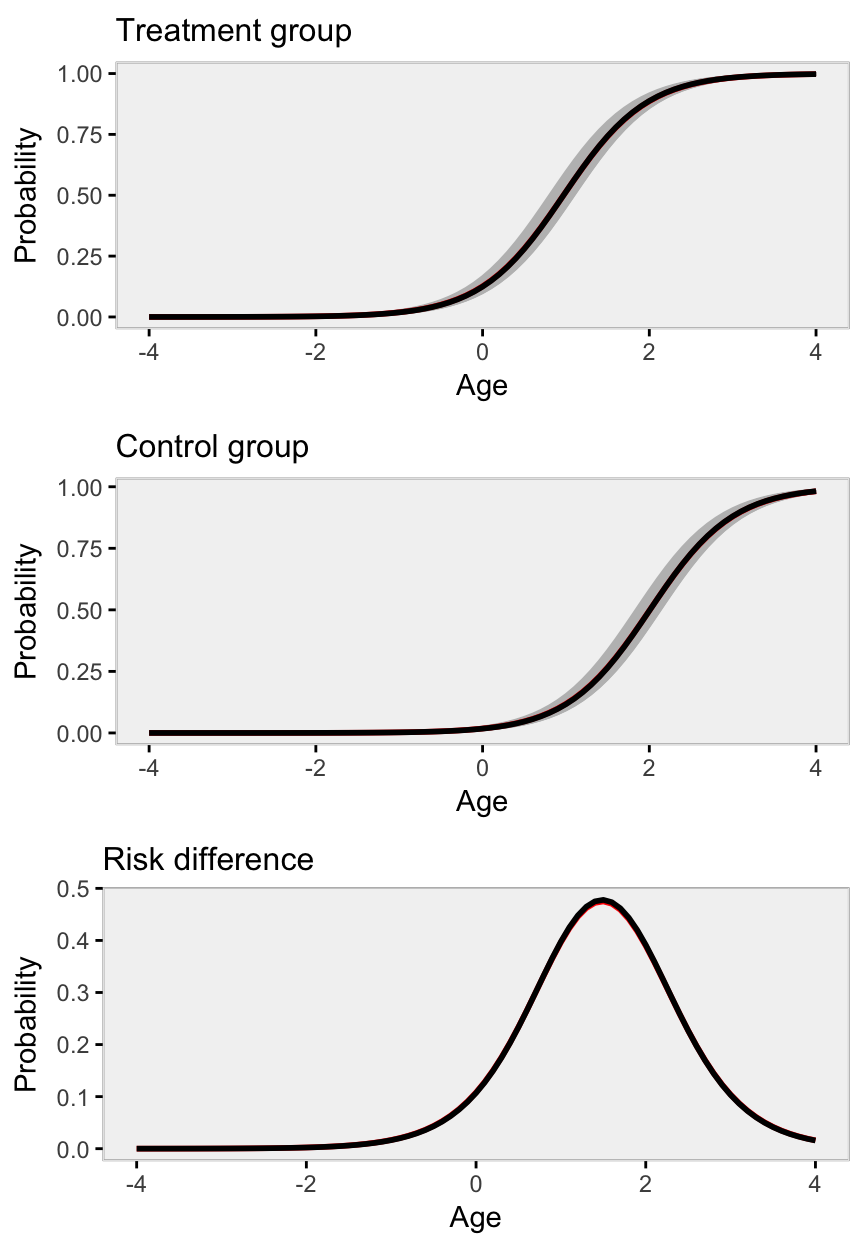
The black lines obscure the red - the marginal model estimate is not much different from the conditional model estimate - because the variance across clusters is negligible.