Any one interested in a function to quickly generate data with many predictors?

A couple of months ago, I was contacted about the possibility of creating a simple function in simstudy to generate a large dataset that could include possibly 10’s or 100’s of potential predictors and an outcome. In this function, only a subset of the variables would actually be predictors. The idea is to be able to easily generate data for exploring ridge regression, Lasso regression, or other “regularization” methods. Alternatively, this can be used to very quickly generate correlated data (with one line of code) without going through the definition process.

I’m presenting a new function here as a work-in-progress. I am putting it out there in case other folks have opinions about what might be most useful; feel free to let me know if you do. If not, I am likely to include something very similar to this in the next iteration of simstudy, which will be version 0.1.16.

Function genMultPred

In its latest iteration, the new function has three interesting arguments. The first two are predNorm and predBin, which are each vectors of length 2. The first value indicates the number of predictors to generate with either a standard normal distribution or a binary distribution, respectively. The second value in each vector represents the number of variables that will actually be predictive of the outcome. (Obviously, the second value cannot be greater than the first value.)

The third interesting argument is corStrength, which is a non-negative number indicating the overall strength of the correlation between the predictors. When corStrength is set to 0 (which is the default), the variables are generated assuming independence. When corStrength is non-zero, a random correlation matrix is generated using package clusterGeneration [Weiliang Qiu and Harry Joe. (2015). clusterGeneration: Random Cluster Generation (with Specified Degree of Separation).] The corStrength value is passed on to the argument ratioLambda in the function genPositiveDefMat. As the value of corStrength increases, higher levels of correlation are induced in the random correlation matrix for the predictors.

Currently, the outcome can only have one of three distributions: normal, binomial, or Poisson.

One possible enhancement would be to allow the distributions of the predictors to have more flexibility. However, I’m not sure the added complexity would be worth it. Again, you could always take the more standard simstudy approach of function genData if you wanted more flexibility.

Here’s the function, in case you want to take a look under the hood:

genMultPred <- function(n, predNorm, predBin, 
                        dist = "normal", sdy = 1, corStrength = 0) {
  
  normNames <- paste0("n", 1:predNorm[1])
  binNames <- paste0("b", 1:predBin[1])
  
  ## Create the definition tables to be used by genData
  
  defn <- data.table(varname = normNames,
                     formula = 0,
                     variance = 1,
                     dist = "normal",
                     link = "identity")
  
  defb <- data.table(varname = binNames,
                     formula = 0.5,
                     variance = NA,
                     dist = "binary",
                     link = "identity")
  
  defx <- rbind(defn, defb)
  attr(defx, which = "id") <- "id"
  
  ## Create the coefficient values - all normally distributed
  
  ncoefs <- rnorm(predNorm[1], 0, 1)
  setzero <- sample(1:predNorm[1], (predNorm[1] - predNorm[2]), 
                    replace = FALSE)
  ncoefs[setzero] <- 0
  
  bcoefs <- rnorm(predBin[1], 0, 1)
  setzero <- sample(1:predBin[1], (predBin[1] - predBin[2]), 
                    replace = FALSE)
  bcoefs[setzero] <- 0
  
  coefs <- c(ncoefs, bcoefs)
  names(coefs) <- c(normNames, binNames)
  
  ## Generate the predictors
  
  if (corStrength <= 0) {     # predictors are independent
    
    dx <- genData(n, defx)
    
  } else {
    
    rLambda <- max(1, corStrength)
    covx <- cov2cor(genPositiveDefMat(nrow(defx), 
                        lambdaLow = 1, ratioLambda = rLambda)$Sigma)
    dx <- genCorFlex(n, defx, corMatrix = covx)
    
  }
  
  ## Generate the means (given the predictors)
  
  mu <- as.matrix(dx[,-"id"]) %*% coefs
  dx[, mu := mu]
  
  ## Generate the outcomes based on the means
  
  if (dist == "normal") {
    dx[, y := rnorm(n, mu, sdy)]
  } else if (dist == "binary") {
    dx[, y := rbinom(n, 1, 1/(1 + exp(-mu)))]  # link = logit
  } else if (dist == "poisson") {
    dx[, y := rpois(n, exp(mu))]               # link = log
  } 
  
  dx[, mu := NULL]
  
  return(list(data = dx[], coefs = coefs))
}

A brief example

Here is an example with 7 normally distributed covariates and 4 binary covariates. Only 3 of the continuous covariates and 2 of the binary covariates will actually be predictive.

library(simstudy)
library(clusterGeneration)

set.seed(732521)

dx <- genMultPred(250, c(7, 3), c(4, 2))

The function returns a list of two objects. The first is a data.table containing the generated predictors and outcome:

round(dx$data, 2)

##       id    n1    n2    n3    n4    n5    n6    n7 b1 b2 b3 b4     y
##   1:   1  0.15  0.12 -0.07 -1.38 -0.05  0.58  0.57  1  1  0  1 -1.07
##   2:   2  1.42 -0.64  0.08  0.83  2.01  1.18  0.23  1  1  0  0  4.42
##   3:   3 -0.71  0.77  0.94  1.59 -0.53 -0.05  0.26  0  0  0  0  0.09
##   4:   4  0.35 -0.80  0.90 -0.79 -1.72 -0.16  0.09  0  0  1  1 -0.58
##   5:   5 -0.22 -0.72  0.62  1.40  0.17  2.21 -0.45  0  1  0  1 -2.18
##  ---                                                                
## 246: 246 -1.04  1.62  0.40  1.46  0.80 -0.77 -1.27  0  0  0  0 -1.19
## 247: 247 -0.85  1.56  1.39 -1.25 -0.82 -0.63  0.13  0  1  0  0 -0.70
## 248: 248  0.72 -0.83 -0.04 -1.38  0.61 -0.71 -0.06  1  0  1  1  0.74
## 249: 249 -0.15  1.62 -1.01 -0.79 -0.53  0.44 -0.46  1  1  1  1  0.95
## 250: 250 -0.59  0.34 -0.31  0.18 -0.86 -0.90  0.22  1  0  1  0 -1.90

The second object is the set of coefficients that determine the average response conditional on the predictors:

round(dx$coefs, 2)

##    n1    n2    n3    n4    n5    n6    n7    b1    b2    b3    b4 
##  2.48  0.62  0.28  0.00  0.00  0.00  0.00  0.00  0.00  0.53 -1.21

Finally, we can “recover” the original coefficients with linear regression:

lmfit <- lm(y ~ n1 + n2 + n3 + n4 + n5 + n6 + n7 + b1 + b2 + b3 + b4, 
            data = dx$data)

Here’s a plot showing the 95% confidence intervals of the estimates along with the true values. The yellow lines are covariates where there is truly no association.

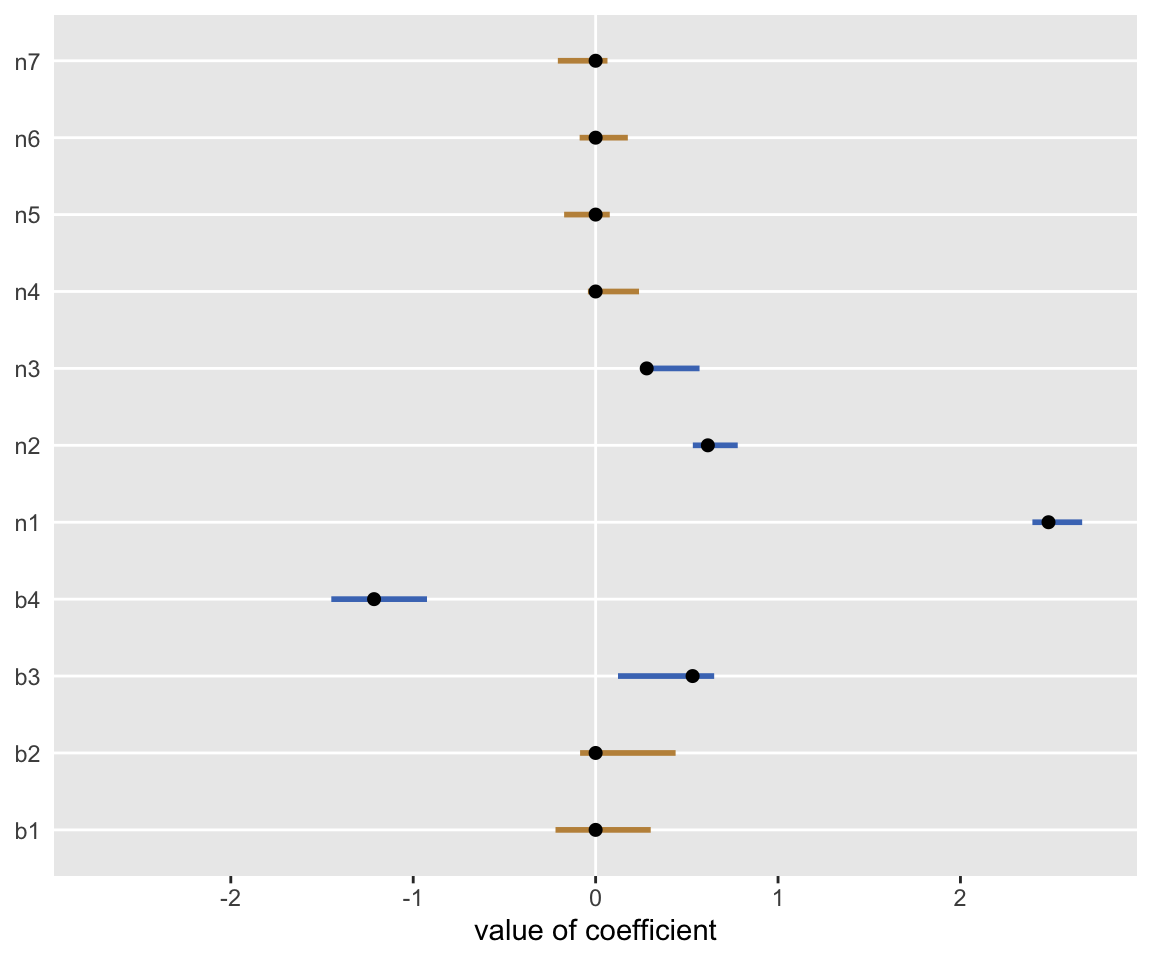
Addendum: correlation among predictors

Here is a pair of examples using the corStrength argument. In the first case, the observed correlations are close to 0, whereas in the second case, the correlations range from -0.50 to 0.25. The impact of corStrength will vary depending on the number of potential predictors.

set.seed(291212)

# Case 1

dx <- genMultPred(1000, c(4, 2), c(2, 1), corStrength = 0)
round(cor(as.matrix(dx$data[, -c(1, 8)])), 2)

##       n1    n2    n3    n4    b1    b2
## n1  1.00 -0.02  0.02  0.03 -0.01 -0.01
## n2 -0.02  1.00 -0.01  0.03 -0.03  0.00
## n3  0.02 -0.01  1.00  0.00 -0.04 -0.01
## n4  0.03  0.03  0.00  1.00  0.06 -0.01
## b1 -0.01 -0.03 -0.04  0.06  1.00 -0.01
## b2 -0.01  0.00 -0.01 -0.01 -0.01  1.00

# Case 2

dx <- genMultPred(1000, c(4, 2), c(2, 1), corStrength = 50)
round(cor(as.matrix(dx$data[, -c(1, 8)])), 2)

##       n1    n2    n3    n4    b1    b2
## n1  1.00  0.09  0.08 -0.32  0.25  0.04
## n2  0.09  1.00 -0.29 -0.47 -0.05 -0.02
## n3  0.08 -0.29  1.00 -0.46 -0.01 -0.01
## n4 -0.32 -0.47 -0.46  1.00 -0.20 -0.05
## b1  0.25 -0.05 -0.01 -0.20  1.00 -0.04
## b2  0.04 -0.02 -0.01 -0.05 -0.04  1.00